若矩形的而积为6cm2,则它的长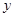 (cm与宽
(cm与宽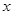 (cm)之间的函数关系用图象表示大致为
(cm)之间的函数关系用图象表示大致为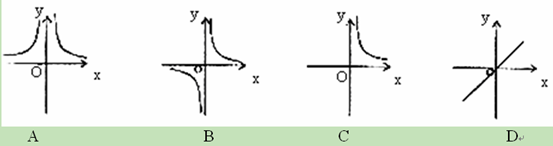
一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(小时),航行的路程为S(千米),则S与t的函数图象大致是( )

(11·十堰)函数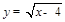 中自变量x的取值范围是( )
中自变量x的取值范围是( )
| A.x≥0 | B.x≥4 | C.x≤4 | D.x>4 |
若a>0,b<-2,则点(a,b+2)应在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得
图形与原图形相比是( ).
| A.向右平移了3个单位 | B.向左平移了3个单位 |
| C.向上平移了3个单位 | D.向下平移了3个单位 |
“罗老师骑自行车上班,最初以某一速度匀速前进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,罗老师加快了速度,仍保持匀速前进,结果准时到校,在课堂上,罗老师请学生画出:自行车行进路程S(千米)和行进时间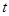 (时)的大致图象,同学们画出的示意图如下,你认为正确的是 ( )
(时)的大致图象,同学们画出的示意图如下,你认为正确的是 ( )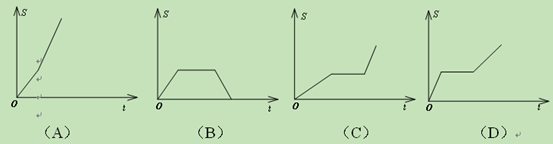
将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是( )
| A.(0,1) | B.(2,﹣1) |
| C.(4,1) | D.(2,3) |
在平面直角坐标系中,下面的点在第一象限的是
| A. | (1,2) | B. | (-2,3) | C. | (0,0) | D. | (-3,-2) |
(11·肇庆)点M ( ,1)关于x轴对称的点的坐标是
,1)关于x轴对称的点的坐标是
A. ( ,1) B. (2.1) C.(2,
,1) B. (2.1) C.(2, ) D (1.
) D (1. )
)
如图,若将直角坐标系中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别变为原来的,则点A的对应点的坐标是【 】
| A.(-4,3) | B.(4,3) | C.(-2,6) | D.(-2,3) |
在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A的坐标为 (-2 , 2 ) ,则点 B’的坐标为
A . ( 3 , 4 ) B . ( 4 , 3 ) C . (一l ,一2 ) D ,(-2,-1)
早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )
| A.小张去时所用的时间多于回家所用的时间 | B.小张在公园锻炼了20分钟 |
| C.小张去时的速度大于回家的速度 | D.小张去时走上坡路,回家时走下坡路 |
(11·柳州)在平面直角坐标系中,将点A (-2,1)向左平移2个单位到点Q,则点Q的坐标为
| A.(-2,3) | B.(0,1) | C.(-4,1) | D.(-4,-1) |
如图,矩形OABC的顶点O为坐标原点,点A在x轴上,点B的坐标为(2,1).如果将矩形OABC绕点O顺时针旋转180°,旋转后的图形为矩形OA1B1C1,那么点B1的坐标为( )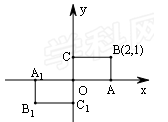
| A.(2,1) | B.(-2,1) | C.(-2,-1) | D.(2,-1) |