初中数学计算器—基础知识试题

小明从家骑车上学，先上坡到达A地后再下坡到达学校，所用的时间与路程如图所示．如果返回时，上、下坡的速度仍然保持不变，那么他从学校回到家需要的时间是（  ）

A．8.6分钟

B．9分钟

C．12分钟

D．16分钟

在同一平面直角坐标系内，将函数的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度，得到图象的顶点坐标是【   】

A．（，1）

B．（1，）

C．（2，）

D．（1，）

如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（－8，0），直线BC经过点B（－8，
6），C（0，6），将四边形OABC绕点O按顺时针方向旋转α度（0＜α≤180°）得到四边形OA′B′C′，
此时直线OA′、直线B′C′分别与直线BC相交于P、Q．在四边形OABC旋转过程中，若BP＝BQ，则点P的坐标为____．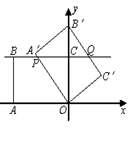

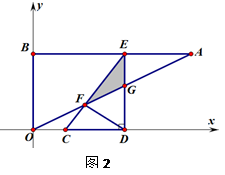
如图1，在平面直角坐标系xOy中，点A，B坐标分别为（8，4），（0，4），线段CD在于x轴上，CD＝3，点C从原点出发沿x轴正方向以每秒1个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E，交OA于点G，连结CE交OA于点F. 设运动时间为t，当E点到达A点时，停止所有运动.
（1）求线段CE的长；
（2）记S为RtΔCDE与ΔABO的重叠部分面积，试写出S关于t函数关系式及t的取值范围；
（3）如图2，连结DF，
1当t取何值时，以C，F，D为顶点的三角形为等腰三角形？
2直接写出ΔCDF的外接圆与OA相切时t的值.

点P（﹣2，1）在平面直角坐标系中所在的象限是【   】

A．第一象限

B．第二象限

C．第三象限

D．第四象限

如图3，点A在双曲线上，且OA＝4，过A作AC⊥轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为(       )

A．

B．5

C．

D．

某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示.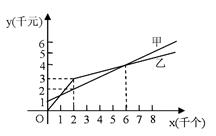

(1) 请你直接写出甲厂的制版费及y_甲与x的函数解析式，并求出其证书印刷单价.
(2) 当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
(3) 如果甲厂想把8千个证书的印制工作承揽下来，在不降低制版费的前提下，每个证书最少降低多少元？

当实数x的取值使得有意义时，函数y=x+1中y的取值范围是（ ▲ )

A．y≥-3

B．y≥-1

C．y>-1

D．y≤-3

若在象棋盘上建立直角坐标系，使“帥”位于点（－1，－2），“馬”位于点（2，－2），则“兵”位于点

A．（－1,1）

B．（－2，－1）

C．（－3,1）

D．（1，－2）

某食堂六月份1日至5日每天用水量变化情况如图所示，那么在这5天内，最多一天的用水量与最少一天的用水量差是        吨.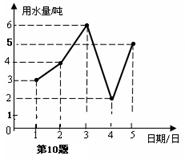

甲、乙二人骑自行车同时从张庄出发，沿同一路线去李庄．甲行驶20分钟因事耽误一会儿，事后继续按原速行驶．下图表示甲、乙二人骑自行车行驶的路程y（千米）随时间x变化的图象（全程），根据图象回答下列问题：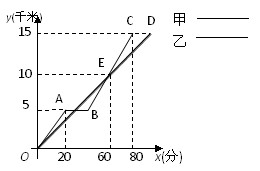

（1）乙比甲晚多长时间到达李庄？
（2）甲因事耽误了多长时间？
（3）x为何值时，乙行驶的路程比甲行驶的路程多1千米？

如图，已知双曲线经过直角三角形OAB斜边OA的中点D，且与直角
边AB相交于点C．若点A的坐标为（，4），则△AOC的面积为(    )   

A．12      B．9      C．6      D．4

图为一位旅行者在早晨８时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：

在这个变化过程中，自变量是____，因变量是______。
９时，１０时３０分，１２时所走的路程分别是多少？
他休息了多长时间？
他从休息后直至到达目的地这段时间的平均速度是多少？

函数的自变量x的取值范围是    (    )

A．x≠0

B．x≠1

C．x≥1

D．x≤1

如图，在以O为原点的平面直角坐标系中，点A、C分别在x轴、y轴的正半轴上，点B(a，b)在第一象限，四边形OABC是矩形，反比例函数y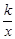＝（k>0，x>0）的图象与AB相交于点D，与BC相交于点E，且BE＝CE．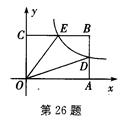

试说明：BD＝AD；
若四边形ODBE的面积是9，求k的值．