若点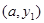 、
、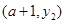 在直线
在直线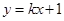 上,且
上,且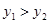 ,则该直线所经过的象限是
,则该直线所经过的象限是 第一、二、三象限
第一、二、三象限  第一、二、四象限
第一、二、四象限  第二、三、四象限
第二、三、四象限  第一、三、四象限
第一、三、四象限
在平面直角坐标系中,已知A(1,1),B(3,3),则在x轴上存在一点C,C到到A、B的距离和最小,此时C的坐标为 .
打开某洗衣机开关,在(洗衣机内无水)洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
已知直线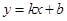 经过点
经过点 、
、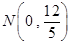 .
.
(1)求直线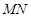 的解析式;
的解析式;
(2)当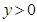 时,求
时,求 的取值范围;
的取值范围;
(3)我们将横坐标、纵坐标均为整数的点称为整数点.直接写出此直线与两坐标轴围成的三角形的内部(不包含边界)的整数点的坐标.
在直角坐标系中,我们把横、纵坐标都为整数的点叫作整点.设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P作向上或向右运动,运动时间(s)与整点(个)的关系如下表:
| 整点P从原点O出发 的时间(s) |
可以得到整点P的坐标 |
可以得到整点 P的个数 |
| 1 |
(0,1),(1,0) |
2 |
| 2 |
(0,2),(1,1),(2,0) |
3 |
| 3 |
(0,3)(1,2)(2,1)(3,0) |
4 |
| … |
… |
… |
根据上表中的规律,回答下列问题:
⑴当整点P从点O出发4s时可得到的整点P有 个;
⑵当整点P从点O出发8s时,在直角坐标系中描出可以得到的整点,并顺次连接这些整点;
⑶当整点P从点O出发 s时,可以到达整点(16,4)的位置;
⑷当整点P(x,y)从点O出发30s时,当整点P(x,y)恰好在直线y=2x-6上,求整点P的坐标.
如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按顺时针方向旋转90°,则点B的对应点的坐标是 .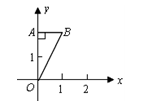
已知点A(0,0),B(3,0),点C在y轴上,且△ABC的面积是6,则点C的坐标为 .
无论实数m取什么值,直线y=x+ m与y=-x+5的交点都不能在( )
m与y=-x+5的交点都不能在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
点A的坐标 满足条件
满足条件 ,则点A的位置在: ( )
,则点A的位置在: ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程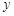 (千米)与所经过的时间
(千米)与所经过的时间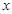 (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程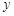 (千米)与所经过的时间
(千米)与所经过的时间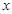 (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
如图所示,函数y1=|x|和 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当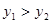 时,x的取值范围是 .
时,x的取值范围是 .
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C(___,___),B→C(___,___),C→(-3,-4);
(2)若贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(-2,-1),(+2,+3),(-1,-2),请在图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1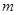 需消牦1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
需消牦1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
函数图象y=ax2+(a-3)x+1与x轴只有一个交点则a的值为 .
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上。OA∥BC,D是BC上一点, ,AB=3, ∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°,设OE=x,AF=y,则y与x的函数关系式为 ,如果△AEF是等腰三角形时。将△AEF沿EF对折得△A′EF与五边形OEFBC重叠部分的面积 。
