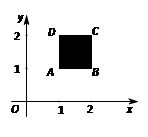初中数学计算器—基础知识试题

如图，图象（折线OEFPMN）描述了某汽车在行驶过程中速度与时间的函数关系，下列说法中错误的是（   ）

A．第3分时汽车的速度是40千米/时

B．第12分时汽车的速度是0千米/时

C．从第3分到第6分，汽车行驶了120千米

D．从第9分到第12分，汽车的速度从60千米/时减少到0千米/时

在函数中，自变量的取值范围是（   ）

A．x≠2

B．x≤-2

C．x≠-2

D．x≥-2

点关于轴对称的点的坐标是     ；点关于原点对称的点的坐标是     ．

施工队准备在一段斜坡上铺上台阶方便通行．现测得斜坡上铅垂的两棵树间水平距离AB=4米，斜面距离BC=4.25米，斜坡总长DE=85米．

（1）求坡角∠D的度数（结果精确到1°）；
（2）若这段斜坡用厚度为17cm的长方体台阶来铺，需要铺几级台阶?

为调动销售人员的积极性，A、B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1～6月份的销售额如下表：

月份 销售额	销售额（单位：元）
1月	2月	3月	4月	5月	6月
小李（A公司）	11600	12800	14000	15200	16400	17600
小张（B公司	7400	9200	1100	12800	14600	16400

（1）  请问小李与小张3月份的工资各是多少？
（2）  小李1～6月份的销售额与月份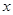的函数关系式是小张1～6月份的销售额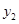也是月份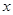的一次函数，请求出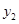与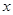的函数关系式；
（3）  如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资。

已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2的速度沿图1的边线运动，运动路径为：，相应的△ABP的面积关于运动时间的函数图像如图2，若，则下列四个结论中正确的个数有【     】
①图1中的BC长是8   ②图2中的M点表示第4秒时的值为24
③图1中的CD长是4   ④图2中的N点表示第12秒时的值为18

A．1个

B．2个

C．3个

D．4个

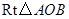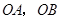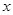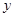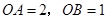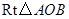如图，在直角坐标系中，的两条直角边分别在轴的负半轴，轴的负半轴上，且．将绕点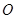按顺时针方向旋转，再把所得的像沿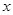轴正方向平移1个单位，得．
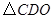（1）写出点的坐标；
（2）求点和点之间的距离．

一个函数的图象关于轴成轴对称图形时，称该函数为偶函数． 那么在下列四个函数①；②；③；④中，偶函数是 　　 （填出所有偶函数的序号）．

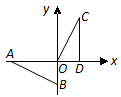
为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）.若设绿化带的BC边长为xm，绿化带的面积为ym².则y与x之间的函数关系式是            ，自变量x的取值范围是           ；

若M(，y₁)、N(，y₂)、P(，y₃)三点都在函数（）的图象上，则y_l、y₂、y₃的大小关系是（    ）

A．y2>y3>y1

B．y2>y1>y3

C．y3>y1>y2

D．y3>y2>y1

函数＋中自变量x的取值范围是（  ）

A．

B．

C．且

D．且

如图，在直角坐标平面内，点与原点的距离，线段与轴正半轴的夹角为，且，则点的坐标是（    ）.

A．（2，3）；	B．（2，）；
C．（，2）；	D．（2，）．

图为一位旅行者在早晨8时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
（1）在这个变化过程中，自变量是     ，因变量是      。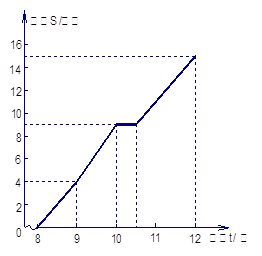

（2）9时，10时，12时所走的路程分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这段时间的平均速度是多少？

已知变量y+1与（x－1）成反比例，且当x=2时，y=0.
（1）求y与x的函数关系式；   （2）若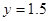，求此时的x值.

如图，有一种动画程序，屏幕上正方形区域ABCD表示黑色物体甲．已知A (1，1)，B (2，1)，C (2，2)，D (1，2)，用信号枪沿直线y =" 2x" + b发射信号，当信号遇到区域甲（正方形ABCD）时，甲由黑变白．则b的取值范围为        时，甲能由黑变白．