初中数学数轴解答题

在数轴上表示下列有理数，并用“＜”号连接起来：
，，0，－2²，－（－3）．

操作探究：已知在纸面上有一数轴（如图所示），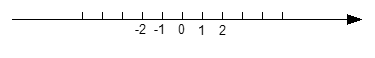

操作一：（1）折叠纸面，使1表示的点与-1表示的点重合，则-3表示的点与______表示的点重合；
操作二：（2） 折叠纸面，使-1表示的点与5表示的点重合，回答以下问题：
①-5表示的点与数_____表示的点重合；
②若数轴上A、B两点之间距离为15，其中A在B的左侧，且A、B两点经折叠后重合，求A、B两点表示的数是多少?
③ 已知在数轴上点M表示的数是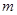，点M到第②题中的A、B两点的距离之和为30，求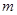的值．

画出数轴，把下列各数：-5、、0、在数轴上表示出来，并用“＜”号从小到大连接．

阅读理解：
阅读下面材料：已知点A、B在数轴上分别表示有理数、，A、B两点之间的距离表示为.当A、B两点中有一点在原点时，不妨设点A在原点，如图1，
当A、B两点都不在原点时，
（1）如图2，点A、B都在原点的右边，

（2）如图3，点A、B都在原点的左边，

（3）如图4，点A、B在原点的两边，

综上，数轴上A、B两点的距离

回答下列问题：
（1） 数轴上表示2和5两点之间的距离是_________.     
数轴上表示-2和-5两点之间的距离是_________.     
数轴上表示-1和3两点之间的距离是_________.    
（2） 数轴上表示和-1的两点A、B之间的距离是_________.     
如果，那么为_________.           
（3） 当代数式取最小值时，相应的x的取值范围是_________.

已知：b是最小的正整数，且a、b满足=0，请回答问题
（1）请直接写出a、b、c的值。
a=__________； b=__________；c=__________
（2）a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x，点P在0到2之间运动时（即0≤x≤2时），请化简式子：（请写出化简过程）

（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB。请问：BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值。

有理数a、b、c在数轴上的对应点如图，化简代数式：=_________．

有理数a，b，c在数轴上的位置如图所示，则|a+c|+|c-b|-|b+a|=（ ）

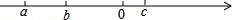
A．-2b

B．0

C．2c

D．2c-2b

如图，甲、乙两人（看成点）分别在数轴和5的位置上，沿数轴做移动游戏．每次移动游戏规则：裁判先捂住一枚硬币，再让两人猜向上一面是正是反，而后根据所猜结果进行移动．

①若都对或都错，则甲向东移动1个单位，同时乙向西移动1个单位；

②若甲对乙错，则甲向东移动4个单位，同时乙向东移动2个单位；

③若甲错乙对，则甲向西移动2个单位，同时乙向西移动4个单位．

（1）经过第一次移动游戏，求甲的位置停留在正半轴上的概率；

（2）从如图的位置开始，若完成了10次移动游戏，发现甲、乙每次所猜结果均为一对一错．设乙猜对次，且他最终停留的位置对应的数为，试用含的代数式表示，并求该位置距离原点最近时的值；

（3）从如图的位置开始，若进行了次移动游戏后，甲与乙的位置相距2个单位，直接写出的值．

结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示4和1的两点之间的距离是         ；表示－3和2两点之间的距离是        ；一般地，数轴上表示数m和数n的两点之间的距离等于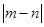．如果表示数a和－2的两点之间的距离是3，那么a＝            ；

（2）若数轴上表示数a的点位于－4与2之间，求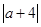+的值；
（3）当a取何值时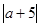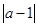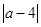，++的值最小，最小值是多少？请说明理由．

如图，在数轴上（未标出原点及单位长度），点A是线段BC的中点．已知点A、B、C所对应的三个数a、b、c之积是负数，这三个数之和与其中一个数相等，请直接写出求、的值．

答：的值是        ，的值是        ．

把下列各数：－2．5，－1²，，－（－3），0在数轴上表示出来，并用“<”把它们连接起来．
 

如图，在数轴上，点 $A$、 $B$分别表示数1、 $-2x+3$．

（1）求 $x$的取值范围；

（2）数轴上表示数 $-x+2$的点应落在　　．

$A$．点 $A$的左边           $B$．线段 $\mathit{AB}$上              $C$．点 $B$的右边

数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．

探究一：求不等式 $|x-1|<2$的解集

（1）探究 $|x-1|$的几何意义

如图①，在以 $O$为原点的数轴上，设点 $A\text{'}$对应的数是 $x-1$，由绝对值的定义可知，点 $A\text{'}$与点 $O$的距离为 $|x-1|$，可记为 $A\text{'}O=|x-1|$．将线段 $A\text{'}O$向右平移1个单位得到线段 $\mathit{AB}$，此时点 $A$对应的数是 $x$，点 $B$对应的数是1．因为 $\mathit{AB}=A\text{'}O$，所以 $\mathit{AB}=|x-1|$．因此， $|x-1|$的几何意义可以理解为数轴上 $x$所对应的点 $A$与1所对应的点 $B$之间的距离 $\mathit{AB}$．

（2）求方程 $|x-1|=2$的解

因为数轴上3和 $-1$所对应的点与1所对应的点之间的距离都为2，所以方程的解为3， $-1$．

（3）求不等式 $|x-1|<2$的解集

因为 $|x-1|$表示数轴上 $x$所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点对应的数 $x$的范围．

请在图②的数轴上表示 $|x-1|<2$的解集，并写出这个解集．

探究二：探究 $\sqrt{{(x-a)}^2+{(y-b)}^2}$的几何意义

（1）探究 $\sqrt{x^2+y^2}$的几何意义

如图③，在直角坐标系中，设点 $M$的坐标为 $(x,y)$，过 $M$作 $\mathit{MP}\perp x$轴于 $P$，作 $\mathit{MQ}\perp y$轴于 $Q$，则 $P$点坐标为 $(x,0)$， $Q$点坐标为 $(0,y)$， $\mathit{OP}=\left|x\right|$， $\mathit{OQ}=\left|y\right|$，在 $\text{Rt}\Delta \text{OPM}$中， $\mathit{PM}=\mathit{OQ}=\left|y\right|$，则 $\mathit{MO}=\sqrt{O{P}^2+P{M}^2}=\sqrt{|x{|}^2+|y{|}^2}=\sqrt{x^2+y^2}$，因此， $\sqrt{x^2+y^2}$ 的几何意义可以理解为点 $M(x,y)$与点 $O(0,0)$之间的距离 $\mathit{MO}$．

（2）探究 $\sqrt{{(x-1)}^2+{(y-5)}^2}$的几何意义

如图④，在直角坐标系中，设点 $A\text{'}$的坐标为 $(x-1,y-5)$，由探究二（1）可知， $A\text{'}O=\sqrt{{(x-1)}^2+{(y-5)}^2}$，将线段 $A\text{'}O$先向右平移1个单位，再向上平移5个单位，得到线段 $\mathit{AB}$，此时点 $A$的坐标为 $(x,y)$，点 $B$的坐标为 $(1,5)$，因为 $\mathit{AB}=A\text{'}O$，所以 $\mathit{AB}=\sqrt{{(x-1)}^2+{(y-5)}^2}$，因此 $\sqrt{{(x-1)}^2+{(y-5)}^2}$的几何意义可以理解为点 $A(x,y)$与点 $B(1,5)$之间的距离 $\mathit{AB}$．

（3）探究 $\sqrt{{(x+3)}^2+{(y-4)}^2}$的几何意义

请仿照探究二（2）的方法，在图⑤中画出图形，并写出探究过程．

（4） $\sqrt{{(x-a)}^2+{(y-b)}^2}$的几何意义可以理解为：　　．

拓展应用：

（1） $\sqrt{{(x-2)}^2+{(y+1)}^2}+\sqrt{{(x+1)}^2+{(y+5)}^2}$的几何意义可以理解为：点 $A(x,y)$与点 $E(2,-1)$的距离和点 $A(x,y)$与点 $F$　　（填写坐标）的距离之和．

（2） $\sqrt{{(x-2)}^2+{(y+1)}^2}+\sqrt{{(x+1)}^2+{(y+5)}^2}$的最小值为　　（直接写出结果）

元旦放假时，小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆．早上从家里出发，向东走了6千米到超市买东西，然后又向东走了1．5千米到爷爷家，中午从爷爷家出发向西走了12千米到外公家，晚上返回家里．
（1）若以家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来；
（2）问超市A和外公家C相距多少千米？
（3）若小轿车每千米耗油0．08升，求小明一家从出发到返回家所经历路程小车的耗油量．（精确到0．1升）

如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

（1）数轴上点B表示的数是      ，点P表示的数是      （用含t的代数式表示）；
（2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q时出发．求：
①当点P运动多少秒时，点P与点Q相遇？
②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？