将 代入反比例函数
代入反比例函数 中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y3,…,如此继续下去,则y2015=________.
中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y3,…,如此继续下去,则y2015=________.
(本小题10分)如图,已知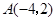 、
、 是一次函数
是一次函数 的图象与反比例函数
的图象与反比例函数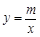
的图象的两个交点.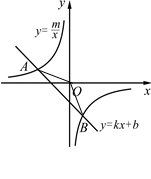
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的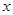 的取值范围.
的取值范围.
如图,已知抛物线 经过点
经过点 、
、 ,交
,交 轴于点
轴于点 .
.
(1)求此抛物线的解析式;
(2)抛物线第一象限上有一动点 ,过点
,过点 作
作 轴,垂足为
轴,垂足为 ,请求出
,请求出 的最大值,及此时点
的最大值,及此时点 坐标;
坐标;
(3)抛物线顶点为 ,
, 轴于
轴于 点,一块三角板直角顶点
点,一块三角板直角顶点 在线段
在线段 上滑动,且一直角边过
上滑动,且一直角边过 点,另一直角边与
点,另一直角边与 轴交于
轴交于 ,请求出实数
,请求出实数 的变化范围,并说明理由.
的变化范围,并说明理由.
沿海开发公司准备投资开发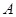 、
、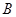 两种新产品,通过市场调研发现:
两种新产品,通过市场调研发现:
(1)若单独投资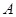 种产品,则所获利润
种产品,则所获利润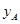 (万元)与投资金额
(万元)与投资金额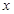 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: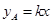 ;
;
(2)若单独投资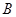 种产品,则所获利润
种产品,则所获利润 (万元)与投资金额
(万元)与投资金额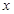 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: .
.
(3)根据公司信息部的报告,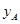 ,
, (万元)与投资金额
(万元)与投资金额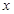 (万元)的部分对应值如下表所示:
(万元)的部分对应值如下表所示:
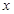 |
1 |
5 |
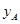 |
0.8 |
4 |
 |
3.8 |
15 |
(1)填空: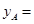 ;
;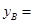 ;
;
(2)若公司准备投资20万元同时开发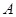 、
、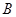 两种新产品,设公司所获得的总利润为
两种新产品,设公司所获得的总利润为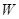 (万元),试写出
(万元),试写出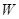 与某种产品的投资金额
与某种产品的投资金额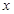 (万元)之间的函数关系式;
(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
当a>0且x>0时,因为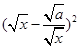 ≥0,所以
≥0,所以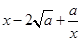 ≥0,从而
≥0,从而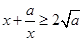 (当
(当 时取等号).记函数
时取等号).记函数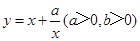 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为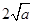 .
.
(1)已知函数y1=x(x>0)与函数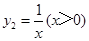 ,则当x= 1 时,y1+y2取得最小值为2 .
,则当x= 1 时,y1+y2取得最小值为2 .
(2)已知函数y1=x+1(x>﹣1)与函数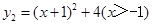 ,求
,求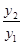 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是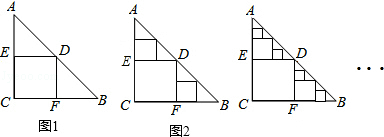
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形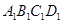 ,
,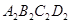 ,
,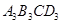 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形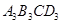 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.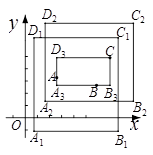
(1)如图1,已知A(-2,0),B(4,3),C(0,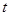 ).
).
①若 ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则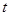 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(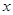 ,
,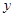 )是抛物线
)是抛物线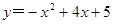 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标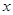 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(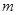 ,
,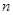 )是函数
)是函数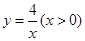 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.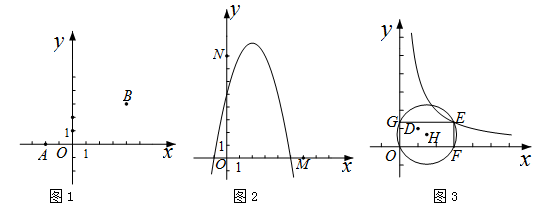
阅读下面材料:
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
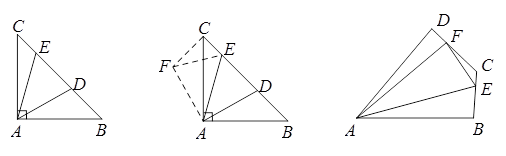
小辉发现,将△ABD绕点A按逆时针方向旋转90º,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是 ,DE的长为 .
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=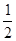 ∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
(1)求∠ADE的度数;
(2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角 (
( ),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求
),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求 的值;
的值;
(3)若图1中∠B= ,(2)中的其余条件不变,判断
,(2)中的其余条件不变,判断 的值是否为定值,如果是,请直接写出这个值(用含
的值是否为定值,如果是,请直接写出这个值(用含 的式子表示);如果不是,请说明理由.
的式子表示);如果不是,请说明理由.
阅读下列材料:
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30°,BC=6,AC=5,在△ABC内部有一点P,连接PA、PB、PC,求PA+PB+PC的最小值.
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD、BE,则BE的长即为所求.

(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60°,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为1,求正方形ABCD的边长.
如图,在平面直角坐标系xOy中,二次函数y=﹣x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
(1)求二次函数的解析式;
(2)连接OE交AB于F点,连接AE,在动点C的运动过程中,若△AOF的面积是△AEF面积的2倍,求点C的坐标?
(3)在动点C的运动过程中,△DEF能否为等腰三角形?若能,请直接写出点F的坐标;若不能,请说明理由.
如图,在平面直角坐标系xOy中,二次函数y=﹣x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
(1)求二次函数的解析式;
(2)连接OE交AB于F点,连接AE,在动点C的运动过程中,若△AOF的面积是△AEF面积的2倍,求点C的坐标?
(3)在动点C的运动过程中,△DEF能否为等腰三角形?若能,请直接写出点F的坐标;若不能,请说明理由.
如图1,正方形ABCD中,点O为对角线AC的中点,点P在直线上AC(不与点O重合),作直线BP,分别作AE⊥BP,CF⊥BP,垂足分别为点E、点F.
(1)求证:△ABE≌△BCF;
(2)如图2,连接OE,OF,判断OE、OF的关系并证明你的结论;
(3)若点P在如图3所示位置,请判断线段AE,OE,CF三者之间的关系,直接写出结论.