北京市石景山区九年级上学期期末考试数学试卷
如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,则sinA的值是( )
A. |
B. |
C. |
D. |
如图,A,B,C都是⊙O上的点,若∠ABC=110°,则∠AOC的度数为( )
| A.70° | B.110° | C.135° | D.140° |
如图,平行四边形ABCD中,E为DC的中点,AC与BE交于点F.则△EFC与△BFA的面积比为( )
A. |
B.1∶2 | C.1∶4 | D.1∶8 |
如图,为测学校旗杆的高度,在距旗杆10米的A处,测得旗杆顶部B的仰角为 ,则旗杆的高度BC为( )
,则旗杆的高度BC为( )
A. |
B. |
C. |
D. |
如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是( )
A. |
B. |
C. |
D. |
如图,△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,那么AE= .
二次函数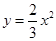 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .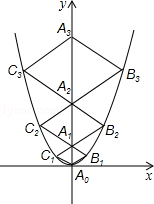
已知:二次函数
(1)若二次函数的图象过点 ,求此二次函数图象的对称轴;
,求此二次函数图象的对称轴;
(2)若二次函数的图象与 轴只有一个交点,求此时
轴只有一个交点,求此时 的值.
的值.
如图,⊙O与割线AC交于点B,C,割线AD过圆心O,且∠DAC=30°.若⊙O的半径OB=5,AD=13,求弦BC的长.
一次函数  与反比例函数
与反比例函数 的图象都过点A
的图象都过点A ,
, 的图象与
的图象与 轴交于点B.
轴交于点B.
(1)求点B坐标及反比例函数的表达式;
(2)C 是
是 轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.
轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.
已知:如图,△ABD中,AC⊥BD于C, ,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色相同,则甲获胜;若两次指针指到的颜色是黄绿组合则乙获胜;其余情况则视为平局.
(1)请用画树状图的方法,列出所有可能出现的结果;
(2)试用概率说明游戏是否公平.
体育测试时,九年级一名男生,双手扔实心球,已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为6m时,达到最大高度5m的B处(如图),问该男生把实心球扔出多远?(结果保留根号)
已知:如图,Rt△AOB中,∠O=90°,以OA为半径作⊙O,BC切⊙O 于点C,连接AC交OB于点P.
(1)求证:BP=BC;
(2)若sin∠PAO= ,且PC=7,求⊙O的半径.
,且PC=7,求⊙O的半径.
阅读下面材料:
(1)小乔遇到了这样一个问题:如图1,在Rt△ABC中,∠C=90°,D,E分别为CB,CA边上的点,且AE=BC,BD=CE,BE与AD的交点为P,求∠APE的度数;
小乔发现题目中的条件分散,想通过平移变换将分散条件集中,如图2,过点B作BF//AD且BF=AD,连接EF,AF,从而构造出△AEF与△CBE全等,经过推理和计算能够使问题得到解决(如图2).请回答:∠APE的度数为___________________.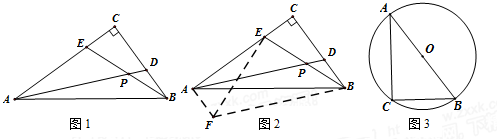
参考小乔同学思考问题的方法,解决问题:
(2)如图3,AB为⊙O的直径,点C在⊙O上,D、E分别为CB,CA上的点,且AE=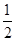 BC,BD=
BC,BD=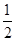 CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
CE,BE与AD交于点P,在图3中画出符合题意的图形,并求出sin∠APE的值.
已知二次函数 在
在 与
与 的函数值相等.
的函数值相等.
(1)求二次函数的解析式;
(2)若二次函数的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,一次函数 经过B,C两点,求一次函数的表达式;
经过B,C两点,求一次函数的表达式;
(3)在(2)的条件下,过动点 作直线
作直线 //x轴,其中
//x轴,其中 .将二次函数图象在直线
.将二次函数图象在直线 下方的部分沿直线
下方的部分沿直线 向上翻折,其余部分保持不变,得到一个新图象M.若直线
向上翻折,其余部分保持不变,得到一个新图象M.若直线 与新图象M恰有两个公共点,请直接写出
与新图象M恰有两个公共点,请直接写出 的取值范围.
的取值范围.
如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
(1)求∠ADE的度数;
(2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角 (
( ),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求
),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求 的值;
的值;
(3)若图1中∠B= ,(2)中的其余条件不变,判断
,(2)中的其余条件不变,判断 的值是否为定值,如果是,请直接写出这个值(用含
的值是否为定值,如果是,请直接写出这个值(用含 的式子表示);如果不是,请说明理由.
的式子表示);如果不是,请说明理由.
如图1,平面直角坐标系 中,点
中,点 ,OC=8,若抛物线
,OC=8,若抛物线 平移后经过C,D两点,得到图1中的抛物线W.
平移后经过C,D两点,得到图1中的抛物线W.
(1)求抛物线W的表达式及抛物线W与 轴另一个交点
轴另一个交点 的坐标;
的坐标;
(2)如图2,以OA,OC为边作矩形OABC,连结OB,若矩形OABC从O点出发沿射线OB方向匀速运动,速度为每秒1个单位得到矩形 ,求当点
,求当点 落在抛物线W上时矩形的运动时间;
落在抛物线W上时矩形的运动时间;
(3)在(2)的条件下,如图3,矩形从O点出发的同时,点P从 出发沿矩形的边
出发沿矩形的边 以每秒
以每秒 个单位的速度匀速运动,当点P到达
个单位的速度匀速运动,当点P到达 时,矩形和点P同时停止运动,设运动时间为
时,矩形和点P同时停止运动,设运动时间为 秒.
秒.
①请用含 的代数式表示点P的坐标;
的代数式表示点P的坐标;
②已知:点P在边 上运动时所经过的路径是一条线段,求点P在边
上运动时所经过的路径是一条线段,求点P在边 上运动多少秒时,点D到CP的距离最大.
上运动多少秒时,点D到CP的距离最大.

 向右平移1个单位后,得到的抛物线的表达式是( )
向右平移1个单位后,得到的抛物线的表达式是( )



 化为
化为 的形式,
的形式, ,
, 的值分别为( )
的值分别为( ) ,
,
 ,
,
 的图象如图所示,下列说法中正确的是( )
的图象如图所示,下列说法中正确的是( )



 时,
时,
 )
) ,使它的图象在各自象限内,
,使它的图象在各自象限内, 的值随
的值随 值的增大而减小,这个函数的表达式为 .
值的增大而减小,这个函数的表达式为 . .
. ,∠ABC=135°,求AC和AB的长.
,∠ABC=135°,求AC和AB的长.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号