初中数学试题

甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人之间的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123．其中正确的是（ ）

A．②③

B．①②③

C．①②

D．①③

已知：点O到△ABC的两边AB，AC所在直线的距离相等，且OB=OC．

（1）如图1，若点O在边BC上，求证：AB=AC；
（2）如图2，若点O在△ABC的内部，求证：AB=AC；
（3）若点O在△ABC的外部，AB=AC成立吗？请画出图表示．

在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S₁，S₂，S₃，S₄，则S₁+S₂+S₃+S₄=     ．

如图，则图中的阴影部分的面积是（ ）

A．12πa^2

B．8πa^2

C．6πa^2

D．4πa^2

如图，一次函数y=x﹣5分别交x轴、y轴于A、B两点，二次函数y=﹣x²+bx+c的图象经过A、B两点．

（1）求二次函数的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（E点位于D点上方），DE=．
①若点D的横坐标为t，用含t的代数式表示D、E的坐标；
②抛物线上是否存在点F，使点F与点D关于x轴对称，如果存在，请求出△AEF的面积；如果不存在，请说明理由．

如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．

（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；
（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；
（3）试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长．

如图，把△ABC绕点B逆时针旋转26°得到△EBF，若EF正好经过A点，则∠BAC=      ．

如图，直线AB：y=﹣x﹣b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．

（1）求点B的坐标；
（2）求直线BC的解析式；
（3）直线EF：y=2x﹣k（k≠0）交AB于E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S_△EBD=S_△FBD？若存在，求出k的值；若不存在，请说明理由．

如图，C为线段AB上一动点（不与点A、B重合），在AB同侧分别作正三角形ACD和正三角形BCE，AE与BD交于点F，AE与CD交于点G，BD与CE交于点H，连接GH．以下五个结论：①AE=BD；②GH∥AB；③AD=DH；④GE=HB；⑤∠AFD=60°，一定成立的有     ．（填序号即可）

如图（1）四边形ABCD中，已知∠ABC+∠ADC=180°，AB=AD，DA⊥AB，点E在CD的延长线上，∠BAC=∠DAE．

（1）求证：△ABC≌△ADE；
（2）求证：CA平分∠BCD；
（3）如图（2），设AF是△ABC的BC边上的高，求证：EC=2AF．

如图，在△ABC中，AB=AC=2，BD=CE，F是AC边上的中点，则AD﹣EF　　1．（填“＞”、“=”或“＜”）

如图，△ABC中，AB=AC，AB的垂直平分线交AC于P点，若AB=5cm，BC=3cm，则△PBC的周长等于（　　）

A．4cm

B．6cm

C．8cm

D．10cm

在我市创建国家级卫生城市中，某社区有一工程需如期完成，在工程招标时，接到甲、乙工程队的投标书，每施工一天，需付甲工程队工程款1.5万元，乙工程队工程款1.1万元．根据甲、乙两队的投标书测算：（1）甲队单独完成这项工程刚好如期完成；
（2）乙队单独完成这项工程要比规定日期多用5天；
（3）若甲、乙两队合做4天，余下的工程有乙队做也正好如期完成．在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？

如图所示的长方体是某种饮料的纸质包装盒，规格为5×6×10（单位：cm），在上盖中开有一孔便于插吸管，吸管长为13cm，小孔到图中边AB距离为1cm，到上盖中与AB相邻的两边距离相等，设插入吸管后露在盒外面的管长为hcm，则h的最小值大约为      cm．
（精确到个位，参考数据：≈1.4，≈1.7，≈2.2）．

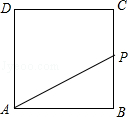
如图，正方形ABCD的边长为4，P为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映y与x的函数关系的是（ ）

A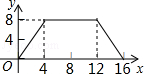．	B．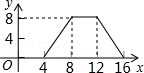
C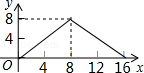．	D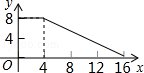．