如图，直线AB：y=﹣x﹣b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．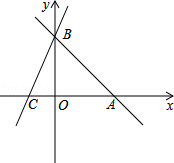
（1）求点B的坐标；
（2）求直线BC的解析式；
（3）直线EF：y=2x﹣k（k≠0）交AB于E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S△EBD=S△FBD？若存在，求出k的值；若不存在，请说明理由．
（贵州六盘水）（本小题16分）如图，已知图①中抛物线
经过点D（-1，0），D（0，-1），E（1，0）．
（1）求图①中抛物线的函数表达式．
（2）将图①中的抛物线向上平移一个单位，得到图②中的抛物线，点D与点D1是平移前后的对应点，
求该抛物线的函数表达式．
（3）将图②中的抛物线绕原点O顺时针旋转90°后得到图③中的抛物线，所得到抛物线表达式为
，点D1与D2是旋转前后的对应点，求图③中抛物线的函数表达式．
将图③中的抛物线绕原点O顺时针旋转90°后与直线
相交于A、B两点，D2与D3是旋转前后如图④，求线段AB的长．
（内蒙古 呼 和 浩 特 ）已知：抛物线y=
+（2m－1）x+
－1经过坐标原点，且当x＜0时，y随x的增大而减小．
（1）求抛物线的解析式，并写出y＜0时，对应x的取值范围;
（2）设点A是该抛物线上位于x轴下方的一个动点，过点A作x轴的平行线交抛物线于另一点D，再作AB⊥x轴于点B， DC⊥x轴于点C．
①当BC=1时，直接写出矩形ABCD的周长;
②设动点A的坐标为（a，b），将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围，判断周长是否存在最大值，如果存在，求出这个最大值，并求出此时点A的坐标;如果不存在，请说明理由．
（黔西南州）如图，在平面直角坐标系中，平行四边形
如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形
．抛物线
经过点A、C、A′三点．
（1）求A、A′、C三点的坐标；
（2）求平行四边形和平行四边形重叠部分
的面积；
（3）点M是第一象限内抛物线上的一动点，问点M在何处时，
的面积最大？最大面积是多少？并写出此时M的坐标．
（内蒙古 呼 和 浩 特 ）如图，在平面直角坐标系中A点的坐标为（8，y），AB⊥x轴于点B, sin∠OAB=
，反比例函数y=
的图象的一支经过AO的中点C，且与AB交于点D．
（1）求反比例函数解析式;
（2）若函数y="3x" 与y=的图象的另一支交于点M，求三角形OMB与四边形OCDB的面积的比．
粤公网安备 44130202000953号