把标准纸一次又一次对开,可以得到形状均相似的“开纸”.现在我们在长为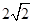 、宽为1的矩形纸片中画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是________.
、宽为1的矩形纸片中画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是________.
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE︰ED=2︰1.如果△BEC的面积为2,那么四边形ABED的面积是________.
如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1.若△E1FA1∽△E1BF,则AD=________.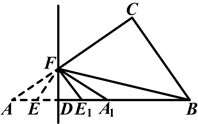
如图,在△ABC中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DF交于点O.若△ADE的面积为S,则四边形BOGC的面积=________.
如图,点A,B的坐标分别是(0,8),(6,0),过边OA上的点P(0,4)作直线PQ与△OAB的另一边相交于点Q,当点Q的坐标为________时,形成的新三角形与△OAB相似.
如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C、D.
①△OB1C∽△OA1D;②OA·OC=OB·OD;③OC·G=OD·F1;④F=F1.上述4个结论中,正确结论有( )
A.1个 B.2个 C.3个 D.4个
如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A. |
B. |
| C.∠ABP=∠C | D.∠APB=∠ABC |
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线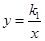 和
和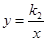 的一个分支上,分别过点A、C作x轴的垂线,垂足分别为M、N,有以下的结论:
的一个分支上,分别过点A、C作x轴的垂线,垂足分别为M、N,有以下的结论:
①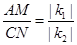 ;
;
②阴影部分的面积是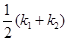 ;
;
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是________(把所有正确结论的序号都填上).
已知P1(x1,y1),P2(x2,y2)是同一个反比例函数图象上的两点,若x2=x1+2.且 ,则这个反比例函数的表达式为________.
,则这个反比例函数的表达式为________.
如图,点A(3,n)在双曲线 上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC的周长是( )
上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC的周长是( )
A.8 B.6 C. D.4
D.4
如图,直线y=m与反比例函数 和
和 的图象分别交于A、B两点,点C是x轴上任意一点,则△ABC的面积为( )
的图象分别交于A、B两点,点C是x轴上任意一点,则△ABC的面积为( )
A.1 B.3 C.4 D.8
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”.例如点(-1,-1),(0,0),(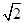 ,
,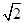 ),……都是“梦之点”,显然,这样的“梦之点”有无数个.
),……都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数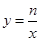 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,y1),B(x2,y2),且满足-2<x1<2,|x1-x2|=2,令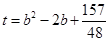 ,试求t的取值范围.
,试求t的取值范围.
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点作x轴的垂线与反比例函数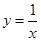 的图象相交于点P1,P2,P3,P4,…,Pn,作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,P5B4⊥A4P4,…,PnBn-1⊥An-1Pn-1,垂足分别为B1,B2,B3,B4,…,Bn-1,连接P1P2,P2P3,P3P4,…,Pn-1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn-1Bn-1Pn,则Rt△Pn-1Bn-1Pn的面积为________.
的图象相交于点P1,P2,P3,P4,…,Pn,作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,P5B4⊥A4P4,…,PnBn-1⊥An-1Pn-1,垂足分别为B1,B2,B3,B4,…,Bn-1,连接P1P2,P2P3,P3P4,…,Pn-1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn-1Bn-1Pn,则Rt△Pn-1Bn-1Pn的面积为________.