如图,水平足够长光滑固定直杆AB上穿有质量为M的滑块,其上用光滑铰链着一个长为L的轻杆,杆的另一端固定着一个质量为M的小球,初始时,系统静止,轻杆水平。1给小球以竖直向上的初速v01,球到达最高点时杆与水平方向呈θ角,(θ<900),求v01。
2给小球以竖直向上的初速v02,球到达最高点时的速度为v,求v02。

如图2所示,光滑水平面上质量为M的平板处于静止状态,其右端的挡板上固定着一轻质弹簧,其光滑的上表面左端放置着一质量为m的小物块。某时刻给小物块一个水平向右的初速度v0,则( )
A 从m接触弹簧到弹簧被压缩得最短的过程中,弹簧的压缩量一定大于M的位移,
B 无论二者质量关系如何,m一定能从M上脱离
C 若M的上表面不光滑且m最终可返回左端,则弹簧最短时m的速度与最终二者的共同速度一定相同,
D 若M的上表面不光滑且m最终可返回左端,则整个运动过程中所产生的热量与弹簧的最大弹性势能相等。
如图1-39所示,一台轧钢机的两个滚子,直径各为d=50cm,以相反方向旋转,滚子间距离为a=0.5cm,如果滚子和热钢间的动摩擦因数为0.1,试求进入滚子前钢板的最大厚度。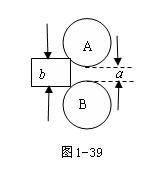
三根不可伸长的相同的轻绳,一端系在半径为r0的环1上,彼此间距相等,绳穿过半径为r0的第2个圆环,另一端同样地系在半径为2r0的环3上,如图1-38所示,环1固定在水平面上,整个系统处于平衡状态.试求第2个环中心与第3个环中心之间的距离.(三个环都是用相同的金属丝制作的,摩擦不计)
如图1-37所示,在竖直平面内固定有两条平行的金属导轨ab、cd,导轨处在与导轨平面垂直的匀强磁场中,磁感应强度B=0.80T,与导轨相连的电源电动势E=3.0V,内阻r=0.5Ω,水平放置的导体棒MN的电阻R=1.5Ω,两端始终与导轨接触良好,且能沿导轨无摩擦滑动,电路中其他电阻不计。当单刀双掷开关S与1接通时,导体棒刚好保持静止状态,求: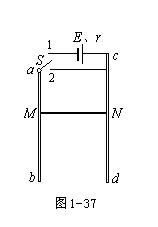
(1)磁场的方向;
(2)当开关S与2接通后,导体棒MN在运动过程中,单位时间(1s)内扫过的最大面积。设导轨足够长。
如图1-35所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球A,球处于静止状态.现对球施加一个方向向右的外力F,使球缓慢偏移,在移动中的每一刻,都可以认为球处于平衡状态.如果外力F方向始终
水平,最大值为2G,试分析:
(1)轻绳张力T的大小取值范围.
(2)在图1-36中画出轻绳张力(T)与cosθ的关系图象.
已知:功率为100W灯泡消耗的电能的5%转化为所发出的可见光的能量,光速 ,普朗克常量
,普朗克常量 ,假定所发出的可见光的波长都是560nm,计算灯泡每秒内发出的光子数。
,假定所发出的可见光的波长都是560nm,计算灯泡每秒内发出的光子数。

如图,一透明半圆柱体折射率为 ,半径为R、长为L。一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出。球该部分柱面的面积S。
,半径为R、长为L。一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出。球该部分柱面的面积S。
麦克斯韦在1865年发表的《电磁场的动力学理论》一文中揭示了电、磁现象与光的内在联系及统一性,即光是电磁波。
(1)一单色光波在折射率为的介质中传播,某时刻电场横波图象如图1所示.求该光波的频率。
(2)图2表示两面平行玻璃砖的截面图,一束平行于边的单色光入射到
界面上,
、
是其中的两条平行光线。光线
在玻璃砖中的光路已给出。画出光线
从玻璃砖中首次出射的光路图.并标出出射光线与界面法线夹角的度数。
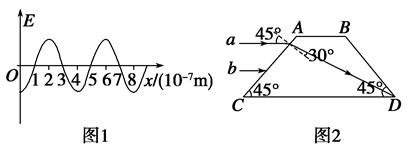

一棱镜的截面为直角三角形ABC,∠A=30o,斜边AB=a。棱镜材料的折射率为n= 。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。
。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。
材料的电阻率ρ随温度变化的规律为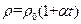 ,其中
,其中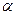 称为电阻温度系数,
称为电阻温度系数,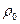 是材料在t="0" ℃时的电阻率,在一定的温度范围内
是材料在t="0" ℃时的电阻率,在一定的温度范围内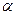 是与温度无关的常量。金属的电阻一般随温度的增加而增加,有正温度系数;而某些非金属如碳等则相反,具有负温数系数。利用具有正负温度系数的两种材料的互补特性,可制成阻值在一定温度范围内不随温度变化的电阻。已知:在0 ℃时,铜的电阻率为
是与温度无关的常量。金属的电阻一般随温度的增加而增加,有正温度系数;而某些非金属如碳等则相反,具有负温数系数。利用具有正负温度系数的两种材料的互补特性,可制成阻值在一定温度范围内不随温度变化的电阻。已知:在0 ℃时,铜的电阻率为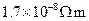 ,碳的电阻率为
,碳的电阻率为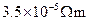 ,在0 ℃附近,铜的电阻温度系数为3.9×10–3 ℃-1,碳的电阻温度系数为
,在0 ℃附近,铜的电阻温度系数为3.9×10–3 ℃-1,碳的电阻温度系数为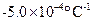 。将横截面积相同的碳棒与铜棒串接成长1.0 m的导体,要求其电阻在0 ℃附近不随温度变化,求所需碳棒的长度(略碳棒和铜棒的尺寸随温度的变化).
。将横截面积相同的碳棒与铜棒串接成长1.0 m的导体,要求其电阻在0 ℃附近不随温度变化,求所需碳棒的长度(略碳棒和铜棒的尺寸随温度的变化).
如图()所示,一个电阻值为
,匝数为
的圆形金属线与阻值为
的电阻
连结成闭合回路。线圈的半径为
. 在线圈中半径为
的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度
随时间
变化的关系图线如图(
)所示。图线与横、纵轴的截距分别为
和
. 导线的电阻不计。求0至
时间内
(1)通过电阻上的电流大小和方向;
(2)通过电阻上的电量
及电阻
上产生的热量。

如图所示,绝缘长方体置于水平面上,两端固定一对平行带电极板,极板间形成匀强电场
。长方体
的上表面光滑,下表面与水平面的动摩擦因数
(设最大静摩擦力与滑动摩擦力相同)。
与极板的总质量
.带正电的小滑块
质量
,其受到的电场力大小
.假设
所带的电量不影响极板间的电场分布。
时刻,小滑块
从
表面上的
点以相对地面的速度
向左运动,同时,
(连同极板)以相对地面的速度
向右运动。问(
取
)
(1)和
刚开始运动时的加速度大小分别为多少?
(2)若最远能到达
点,
、
的距离L应为多少?从
时刻至
运动到
点时,摩擦力对
做的功为多少?

如图所示,水平地面上静止放置着物块,相距
。物块
以速度
沿水平方向与
正碰。碰撞后
牢固地粘在一起向右运动,并再与
发生正碰,碰后瞬间
的速度
。已知
的质量均为
,
的质量为
质量的
倍,物块与地面的动摩擦因数
,
取
)

(1)计算与碰撞前瞬间
的速度;
(2)根据的碰撞过程分析
的取值范围,并讨论与
碰撞后
的可能运动方向。
如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为、足够长且电阻忽略不计,导轨平面的倾角为
,条形匀强磁场的宽度为
,磁感应强度大小为
、方向与导轨平面垂直。长度为
的绝缘杆将导体棒和正方形的单匝线框连接在一起组成"
 "型装置,总质量为
"型装置,总质量为,置于导轨上。导体棒中通以大小恒为
的电流(由外接恒流源产生,图中未图出)。线框的边长为
,电阻为
,下边与磁场区域上边界重合。将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直。重力加速度为
。
求:(1)装置从释放到开始返回的过程中,线框中产生的焦耳热;
(2)线框第一次穿越磁场区域所需的时间;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离。
