高中物理综合题

挡板P中嵌有一块如图所示的球形玻璃砖,玻璃砖折射率为,在球心O点处有一点光源S,E为光屏,相关数据下图.求:

(1)光屏上被照亮部分圆的半径;
(2)若把玻璃砖的外侧面AB切成平面,则光屏上被照亮部分的面积如何变化，为什么?

为从军事工事内部观察外面的目标，在工事壁上开一长方形孔.设工事壁厚d="34.64" cm，孔的宽度L="20" cm，孔内嵌入折射率的玻璃砖，如图15-15所示.试问：
（1）嵌入玻璃砖后，工事内部人员观察到外界的视野的最大张角为多少？
（2）要想使外界180°范围内景物全被观察到，应嵌入多大折射率的玻璃砖？

图15-15

如图12所示，游泳池宽度L="15" m，水面离岸边的高度为0.5 m，在左岸边一标杆上装有一A灯，A灯距地面高0.5 m，在右岸边站立着一个人，E点为人眼的位置，人眼距地面高1.5 m.若此人发现A灯经水面反射所成的像与左岸水面下某处的B灯经折射后所成的像重合，已知水的折射率为1.3，则B灯在水面下多深处？（B灯在图中未画出）

图12

如图11所示，AOB是1/4圆柱玻璃砖的截面图.玻璃的折射率为，今有一束平行光线以45°的入射角入射到玻璃砖的AO面，这些光线只有一部分能从AB面射出，并假设凡是射到OB面上的光线全部被吸收，也不考虑OA面的反射作用.试求圆柱AB面上能射出光线的面积占AB表面积的几分之几?

图11


如图15-17所示为一直光导纤维，AB之间距离为s,使一光脉冲信号从光导纤维中间入射，射入后在光导纤维与空气的界面上恰好发生全反射，由A点传输到B点所用时间为t，求光导纤维所用材料的折射率.

图15-17

科学家设想在未来的航天事业中用太阳帆来加速星际宇宙飞船，按照近代光的粒子说，光由光子组成，飞船在太空张开太阳帆，使太阳光垂直射到太阳帆上，太阳帆面积为S，太阳帆对光的反射率为100%，设太阳帆上每单位面积接受太阳光的辐射功率为P（即单位时间t₀内有Pt₀的光能到达）.已知每个光子动量为hνc（式中h为普朗克常量,ν为光频率,c为光速），则:
（1）若飞船总质量为m，求飞船加速度的表达式.
（2）如果太阳帆对阳光一面是黑色，可以完全吸收太阳光，则飞船加速度表达式又是怎么样的？

一光电管的阴极用极限波长λ₀="5" 000×10^-8 m的钠制成.用波长λ="3" 000×10^-8 m的紫外线照射阴极，光电管阳极A和阴极K之间的电势差U="2.1" V,光电流的饱和值I="0.56" μA.
（1）求每秒内由K极发射的电子数；
（2）求电子到达A极时的最大动能；
（3）如果电势差U不变,而照射光的强度增到原值的3倍，此时电子到达A极时的最大动能是多大?(普朗克常量h=6.63×10^－34 J·s,电子电荷量e=1.60×10^－19 C,真空中的光速c=3.00×10⁸ m/s)


利用如图14所示的装置可测量弹簧的劲度系数.一小平面镜B（可视为一点）竖直固定在物块P上，它们的总质量为m.现将P紧靠着直立的弹簧上端，用插销K固定，此时弹簧处于自然长度，从固定的点光源S发出的光经过平面镜反射后在竖直标尺的A点形成一小光斑.松开插销K，发现最终小光斑稳定在标尺上某点，该点到A点的距离为h.已知点光源S与平面镜的水平距离为L₀，标尺与平面镜的水平距离为L，求该弹簧的劲度系数.

图14

如图15-25所示，游泳池宽度L="15" m，水面离岸边的高度为0.5 m，在左岸边一标杆上装有一A灯，A灯距地面高0.5 m，在右岸边站立着一个人，E点为人眼的位置，人眼距地面高1.5 m.若此人发现A灯经水面反射所成的像与左岸水面下某处的B灯经折射后所成的像重合，已知水的折射率为1.3，则B灯在水面下多深处？（B灯在图中未画出）

玻璃棱镜ABCD可以看成是由如图15-24所示的ADE、ABE、BCD三个直角三棱镜组成的，一束从AD面入射的光线在棱镜中的折射光线ab与AD面的夹角α＝60°，已知光在真空中的传播速度c＝3×10⁸ m/s，玻璃的折射率n＝1.5.求：

图15-24
（1）这束入射光线的入射角多大？（用反三角函数表示）
（2）光在棱镜中的传播速度多大？
（3）该束光线第一次从CD面出射时的折射角以及此出射光线的偏向角（射出棱镜的光线与射入棱镜的光线之间的夹角）多大？
（解题过程要画出解题所需的完整光路图）

图15-25

如图15-31所示，一等腰直角棱镜，放在真空中，AB=AC=d.在棱镜侧面AB左方有一单色点光源S，从S发出的光线SD以60°的入射角从AB侧面中点射入，当它从AC侧面射出时，出射光线偏离入射光线的偏向角为30°，若测得光从光源到棱镜侧面AB的时间跟在棱镜中传播时间相等，那么点光源S到棱镜AB侧面的垂直距离是多少？

图15-31

半径为R的玻璃半圆柱体，横截面如图13-4-8所示，圆心为O，两条平行单色红光沿截面射向圆柱面，方向与底面垂直，光线1的入射点A为圆柱面的顶点，光线2的入射点为B，∠AOB=60°，已知该玻璃对红光的折射率n=.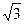

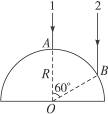
图13-4-8
（1）求两条光线经柱面和底面折射后的交点与O点的距离d；
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小?

为了减少光在透镜表面由于反射带来的损失,可在透镜表面涂上一层增透膜.已知增透膜的折射率为1.4,绿光的波长为5 600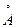.为了使其在垂直表面入射的使反射光干涉消失,求所涂的这种增透膜的最小厚度.

如图19-4-15所示，宽为a的平行光束从空气斜射到两面平行的玻璃板上表面，入射角为45°.光束中包含两种波长的光，玻璃对这两种波长光的折射率分别为n₁=1.5,n₂=.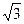

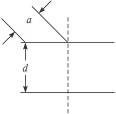
图19-4-15
（1）求每种波长的光射入上表面后的折射角r₁、r₂.
（2）为使光束玻璃下表面出射时能分成不交叠的两束，玻璃板的厚度d至少为多少？并画出光路示意图.

如图19-4-12所示，等腰直角棱镜ABO的两腰长都是16 cm.为了测定它的折射率，棱镜放在直角坐标系中，使两腰与Ox、Oy轴重合.从OB边的C点注视A棱，发现A棱的视位置在OA边上的D点，在C、D两点插上大头针，看出C点的坐标为（0，12），D点的坐标为（9，0）.由此计算出该棱镜的折射率为多少？