高中物理综合题

太阳内部持续不断地发生着4个质子聚变为1个氦核的热核反应，这个核反应释放出的大量能量就是太阳的能源.
(1)写出这个核反应方程；
(2)这一核反应能释放多少能量？
(3)已知太阳每秒释放的能量为3.8×10²⁶ J，则太阳每秒减少的质量为多少？
(4)若太阳质量减少万分之三，热核反应不能继续进行，计算太阳能存在多少年.(太阳质量M＝2×10³⁰ kg,m_p＝1.007 3 u，m_He＝4.001 5 u，m_e＝0.000 55 u)

在可控核反应堆中需要给快中子减速，轻水、重水和石墨等常用作减速剂.中子在重水中可与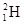核碰撞减速，在石墨中与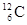核碰撞减速.上述碰撞可简化为弹性碰撞模型.某反应堆中快中子与静止的靶核发生对心正碰，通过计算说明，仅从一次碰撞考虑，用重水和石墨作减速剂，哪种减速效果更好？

太阳现正处于主序星演化阶段.它主要是由正、负电子和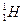、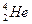等原子核组成的，维持太阳辐射的是它内部的核聚变反应，核反应方程是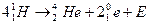（释放的核能），这些核能最后转化为辐射能.根据目前关于恒星演化的理论，若由于聚变反应而使太阳中的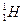核数目从现有数减少10％，太阳将离开主序星阶段而转入红巨星的演化阶段，为了简化，假定目前太阳全部由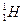核组成.
（1）为了研究太阳演化进程，需知道目前太阳的质量M，已知地球半径R＝6.4×10⁶ m，地球质量m＝6.0×10²⁴ kg，日地中心的距离r＝1.5×10¹¹ m，地球表面处的重力加速度g＝10 m／s²，1年约为3.2×10⁷ s，试估算目前太阳的质量M.
（2）已知质子质量m_p＝1.672 6×10^-27kg，He质量m_α＝6.645 8×10 ^-27 kg，电子质量m_e＝0.9×10^-30 kg，光速c＝3×10⁸ m／s，求每发生一次题中所述的核聚变反应所释放的核能.
（3）已知地球上与太阳光垂直的每平方米截面上，每秒通过的太阳辐射能W＝1.35×10³ J／m²，试估算太阳继续保持在主序星阶段还有多少年的寿命.（估算结果只要求一位有效数字）

如图17-14所示，某一足够大的真空中，虚线PH右侧是磁感应强度为B、方向垂直于纸面向里的匀强磁场，左侧是一场强为E、方向水平向左的匀强电场.静止于虚线PH上的一点O处的镭核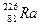水平向右放出一个α粒子而衰变成氡核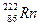.设α粒子与氡核分离后它们之间的作用可忽略不计，涉及动量问题时亏损的质量不计，重力不计.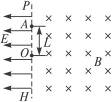

图17-14
（1）写出镭核衰变的核反应方程;
（2）若经过一段时间，α粒子刚好到达虚线PH上的A点，测得OA＝L，求此时氡核的速率.（已知α粒子的比荷为b）

1930年科学家发现钋放出的射线贯穿能力极强，它甚至能穿透几厘米厚的铅板，1932年，英国年轻物理学家查德威克用这种未知射线分别轰击氢原子和氮原子，结果打出一些氢核和氮核.若未知射线均与静止的氢核和氮核正碰，测出被打出的氢核最大速度为v_H＝3.5×10⁷ m／s，被打出的氮核的最大速度v_N＝4.7×10⁶m／s，假定正碰时无机械能损失，设未知射线中粒子质量为m，初速为v，质子的质量为m′.
（1）推导被打出的氢核和氮核的速度表达式；
（2）根据上述数据，推算出未知射线中粒子的质量m与质子的质量m′之比.（已知氮核质量为氢核质量的14倍）

如图17-12所示，静止在匀强磁场中的⁶₃Li核俘获一个速度为v₀＝7.7×10⁴ m／s的中子而发生核反应，，若已知He的速度为v₂＝2.0×10⁴ m／s，其方向跟中子反应前的速度方向相同，求：

图17-12
（1）的速度是多大？
（2)在图中画出粒子和的运动轨迹，并求它们的轨道半径之比.
（3）当粒子旋转了3周时，粒子旋转几周？

已知氘核质量为2.013 6 u，中子质量为1.008 7 u,He的质量为3.015 0 u.
(1)写出两个氘核聚变成He的核反应方程；
(2)计算上述核反应中释放的核能；
(3)若两氘核以相等的动能0.35  MeV做对心碰撞即可发生上述核反应，且释放的核能
全部转化为机械能，则反应中生成的He和中子的动能各是多少?

已经证实，质子、中子都是由上夸克和下夸克两种夸克组成的，上夸克带电为e,下夸克带电为-e,e为电子所带电荷量的大小，如果质子是由三个夸克组成的，且各个夸克之间的距离都为l,l=1.5×10^-15 m，试计算质子内相邻两个夸克之间的静电力（库仑力）.

铋核（Bi）要放出一个α粒子变成另一个粒子，已知α粒子动能为89.5×10^-5 eV，另一粒子动能为22.5×10⁵ eV，则（不计反冲核动能）
（1）完成核反应方程；
（2）1 g铋212全部衰变成铅208所放出的能量是多少？

为确定爱因斯坦质能联系方程ΔE=Δmc²的正确性，设计了如下实验：用动能为E₁="0.9 " MeV的质子去轰击静止的锂核Ｌi，生成两个α粒子，测得这两个α粒子的动能之和为E="19.9" MeV.
(1)写出该核反应方程；
(2)计算核反应过程中释放出的能量ΔE；
(3)通过计算说明ΔE=Δmc²的正确性.(计算中质子、α粒子和锂核Ｌi的质量分别取：m_p="1.007" 3  u，m_α="4.001" 5  u，m_Ｌi="7.016" 0  u)

原子在不停地做热运动，为了能高精度地研究孤立原子的性质，必须使它们几乎静止下来并能在一个很小的空间区域停留一段时间，例如纳米技术中需要移动或修补分子.科学家已发明了一种称为“激光制冷”的技术，原理如下：
在一个真空室内，一束非常准直的Na-23原子束（通过样品在1 000 K高温下蒸发而获得，原子做热运动的速率近似为v₀="1" 000 m/s),受一束激光的正面照射，如图15-2-3所示.设原子处在基态，运动方向与激光光子的运动方向相反，选好激光频率使光子能量E等于钠原子第一激发态与基态间能量差，原子就能吸收它而发生跃迁，跃迁后原子的速度为v₁，随后该原子发射光子并回到基态.设所发射光子的运动方向与速度v₀的方向总是相同的，此时原子的速度为v₂,接着重复上述过程，直到原子的速度减小到零.

图15-2-3
（1）吸收与发射光子的总次数为多少？
（2）原子停留在激发态上的时间称为原子在这种状态下的寿命，大小约为10^-8 s.忽略每次吸收与发射光子的时间，按上述方式，原子初速度v₀减小到零，共需多长时间？该时间内原子共走过的路程为多少？（E=3.36×10^-19 J，钠原子的质量m=3.84×10^-26 kg,N_A=6.0×10²³ mol^-1,c=3.0×10⁸ m/s）

静止状态的镭原子核Ra经α衰变后变成一个新核.
（1）写出核衰变方程；
（2）若测得放出的α粒子的动能为E_k1，求反冲核动能E_k2及镭核衰变时放出的总能量E.

地球的年龄到底有多大，科学家们是利用天然放射性元素的衰变规律来推测的.通过对目前发现的最古老的岩石中铀和铅含量的测定，测定出该岩石中含有的铀是岩石形成初期时（岩石形成初期不含铅）的一半.铀238衰变后形成铅206，铀238的相对含量随时间的变化规律如下图所示.图中N为铀238的原子数，N₀为铀和铅的总原子数，则由此可以断定：

（1）地球年龄大约为多少年？
（2）被测定的古老岩石样品在90亿年后的铀、铅原子数之比是多少？

如图19-4-2所示是工厂利用放射线自动控制铝板厚度的装置示意图．

图19-4-2
(1)请简述自动控制原理．
(2)如果工厂生产的是厚度为1 mm的铝板，在α、β和γ三种射线中，哪一种对铝板的厚度起主要控制作用，为什么?

氢原子中电子离核最近的轨道半径r₁=0.53×10^-10 m，试计算在此轨道上电子绕核转动的频率和加速度（已知电子质量m_e=0.91×10^-30 kg).