在广口瓶内盛满水，像图19-2-16那样把直尺AB紧挨着广口瓶的C点竖直插入瓶内，这时在直尺对面的P点观察水面，能同时看到直尺在水中的部分和露出水面部分的像.若看到的直尺水下部分最低点的刻度S1以及跟这个刻度相重合的水上部分的刻度S2的像S2′，已知：S1的位置坐标为4 cm,S0的位置坐标为20 cm，S2的位置坐标为29 cm，广口瓶直径d为12 cm，根据以上数据，求出水的折射率.
图19-2-16
光线以入射角i从空气射向折射率n=
的透明介质表面，如图19-2-14.
图19-2-14
(1)当入射角i=45°时，求反射光线与折射光线的夹角θ.
(2)当入射角i为何值时，反射光线与折射光线间的夹角θ=90°?
用折射率为n的透明物质做成内、外半径分别为a、b的空心球，如图所示，球的内表面涂有能完全吸收光的物质.则当一平行光射向此球时，球吸收的光束的横截面积多大（指光束进入空心球前的横截面积）？
一般认为激光器发出的是频率为v的“单色光”，实际上它的频率并不是真正单一的.激光频率v是它的中心频率，它所包含的频率范围是Δv（也称频率宽度）.如图所示，让单色光照射到薄膜表面a，一部分光从上表面反射回去（这部分光称为甲光），其余的光进入薄膜内部，其中的一小部分光从薄膜下表面b反射回来，再从上表面折射出去(这部分光称为乙光）.当甲、乙这两部分光相遇叠加而发生干涉，称为薄膜干涉.乙光与甲光相比，要在薄膜中多传播一小段时间Δt.理论和实践都证明,能观察到明显稳定的干涉现象的条件是:Δt的最大值Δtm与Δv的乘积近似等于1,即只有满足Δtm·Δv≈1才会观察到明显稳定的干涉现象.已知某红宝石激光器发出的激光频率v=4.32×1014 Hz,它的频率宽度Δv=8.0×109 Hz.让这束激光由空气斜射到折射率n=2的液膜表面,入射光与液膜表面成45°角,如图所示.求：
（1）从O点射入薄膜中的光的传播速率；
（2）估算在如图所示的情景下，能观察到明显稳定干涉现象的液膜的最大厚度dm.
金属钠蒸气发出的黄光，频率是5.1×1014 Hz，它以45°的入射角由空气射入玻璃后，折射角是30°，那么它在玻璃中的传播速度和波长如何改变？改变了多少？
要使某透镜能对在空气中波长为0.52 μm的黄绿光增透，至少要在镜面上涂厚度为多大的增透膜?（假定做这种膜的材料的折射率为1.3）
一束单色光，在真空中的波长是6.00×10-7 m，当它进入玻璃中传播时速度变为2.00×108m/s，则该玻璃的折射率是多少？它在玻璃中的波长是多少？频率是多少？
一个氦氖激光器能发出4.74×1014 Hz的红光.求：
（1）它在真空中的波长.
（2）进入折射率为
的透明介质中，这束激光的波长、波速又是多少？
中国科学院上海光学精密机械研究所在一个不到10m2的光学平台上，在35 fs(fs是一种时间单位，读作飞秒.1 fs=10-15s )的超短瞬间内获得了15×1012W的超强超短激光束．这一瞬时功率相当于全世界所有电网功率总量的数倍．据了解，自然界中类似的极端物理条件，只有在核爆中心、恒星内部以及黑洞边缘才能找到．在实验室中用人工手段获得这种条件，意味着人类在激光研究领域将进入一个前所未有的超强超快的境界．通过以上叙述，计算在这35 fs中所释放的激光能量是多少.
如图14-1-23所示，一等腰直角棱镜，放在真空中，AB=AC=d.在棱镜侧面AB左方有一单色点光源S，从S发出的光线SD以60°的入射角从AB侧面中点射入，当它从AC侧面射出时，出射光线偏离入射光线的偏向角为30°.若测得光从光源到棱镜侧面AB的时间跟在棱镜中传播时间相等，那么点光源S到棱镜AB侧面的垂直距离是多少？
图14-1-23
如图14-1-22所示，巡查员站立于一空的贮液池边，检查池角处出液口的安全情况.已知池宽为L，照明灯到池底的距离为H.若保持照明光束方向不变，向贮液池中注入某种液体，当液面高为
时，池底的光斑距离出液口
图14-1-22
(1)试求当液面高为
时，池底的光斑到出液口的距离x.
(2)控制出液口缓慢地排出液体，使液面以vh的速率匀速下降，试求池底的光斑移动的速率vx.
用波长λ="0.51" μm的绿光做双缝干涉实验,测得相邻两条亮纹间的距离Δx="0.55" mm.若将整个装置放入折射率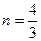
的水中,那么相邻两条亮纹间的距离是多大?
如图13-21所示，横截面是直角三角形ABC的三棱镜对红光的折射率为n1，对紫光的折射率为n2。一束很细的白光由棱镜的一个侧面AB垂直射入，从另一侧面AC折射出来。已知棱镜顶角∠A=30°，AC边平行于光屏MN，且与光屏的距离为L。
图13-21
(1)画出白光通过棱镜的光路图(出射光线只画出两条边缘光线，并指明其颜色)。
(2)求在光屏MN上得到的彩色光带的宽度d。
粤公网安备 44130202000953号