高中物理解答题

如图所示，带电量分别为和的小球、固定在水平放置的光滑绝缘细杆上，相距为。若杆上套一带电小环，带电体、和均可视为点电荷。
（1）求小环的平衡位置。

（2）若小环带电量为，将小环拉离平衡位置一小位移后静止释放，试判断小环能否回到平衡位置。（回答"能"或"不能"即可）

（2）若小环带电量为，将小环拉离平衡位置一小位移后静止释放，试证明小环将作简谐运动。（提示：当时，则 ）

图丙是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片，照相机的镜头竖直向上。照片中，水立方运动馆的景象呈现在半径的圆型范围内，水面上的运动员手到脚的长度，若已知水的折射率为，请根据运动员的实际身高估算该游泳池的水深，（结果保留两位有效数字）

有两个完全相同的小滑块和，沿光滑水平面以速度与静止在平面边缘点的发生正碰，碰撞中无机械能损失。碰后运动的轨迹为曲线，如图所示。

（1）已知滑块质量为,碰撞时间为，求碰撞过程中对平均冲力的大小。

（2）为了研究物体从光滑抛物线轨道顶端无初速下滑的运动，特制做一个与平抛轨道完全相同的光滑轨道，并将该轨道固定在与曲线重合的位置，让沿该轨道无初速下滑（经分析，下滑过程中不会脱离轨道）。
a.分析沿轨道下滑到任意一点的动量与平抛经过该点的动量的大小关系;

b.在曲线上有一点，和两点连线与竖直方向的夹角为45°。求通过点时的水平分速度和竖直分速度。

用插针法测量上、下表面平行的玻璃砖的折射率。实验中用A、B两个大头针确定入射光路，C、D两个大头针确定出射光路， $O$ 和 $O\text{'}$ 分别是入射点和出射点。如图（a）所示。测得玻璃砖厚度为 $h＝15.0\mathit{mm}$ ；A到过 $O$ 点的法线 $\mathit{OM}$ 的距离 $\mathit{AM}＝10.0\mathit{mm}$ ， $M$ 到玻璃砖的距离 $\mathit{MO}＝20.0\mathit{mm}$ ， $O\text{'}$ 到 $\mathit{OM}$ 的距离为 $s＝5.0\mathit{mm}$ 。

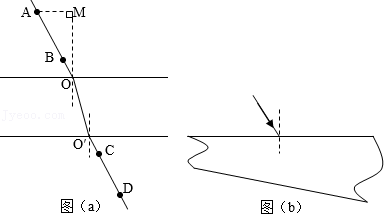
（ⅰ）求玻璃砖的折射率；

（ⅱ）用另一块材料相同，但上下两表面不平行的玻璃砖继续实验，玻璃砖的截面如图（b）所示。光从上表面入射，入射角从 $0$ 逐渐增大，达到 $45°$ 时，玻璃砖下表面的出射光线恰好消失。求此玻璃砖上下表面的夹角。

如图所示，两足够长的光滑金属导轨竖直放置，相距为,一理想电流表与两导轨相连，匀强磁场与导轨平面垂直.一质量为、有效电阻为的导体棒在距磁场上边界处静止释放.导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为。整个运动过程中，导体棒与导轨接触良好，且始终保持水平，不计导轨的电阻。求：

（1）磁感应强度的大小；
（2）电流稳定后，导体棒运动速度的大小；
（3）流经电流表电流的最大值

如图，长度均为 l的两块挡板竖直相对放置，间距也为 l，两挡板上边缘 P和 M处于同一水平线上，在该水平线的上方区域有方向竖直向下的匀强电场，电场强度大小为 E；两挡板间有垂直纸面向外、磁感应强度大小可调节的匀强磁场。一质量为 m，电荷量为 q（ q＞0）的粒子自电场中某处以大小为v ₀的速度水平向右发射，恰好从 P点处射入磁场，从两挡板下边缘 Q和 N之间射出磁场，运动过程中粒子未与挡板碰撞。已知粒子射入磁场时的速度方向与 PQ的夹角为60°，不计重力。

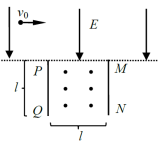
（1）求粒子发射位置到 P点的距离；

（2）求磁感应强度大小的取值范围；

（3）若粒子正好从 QN的中点射出磁场，求粒子在磁场中的轨迹与挡板 MN的最近距离。

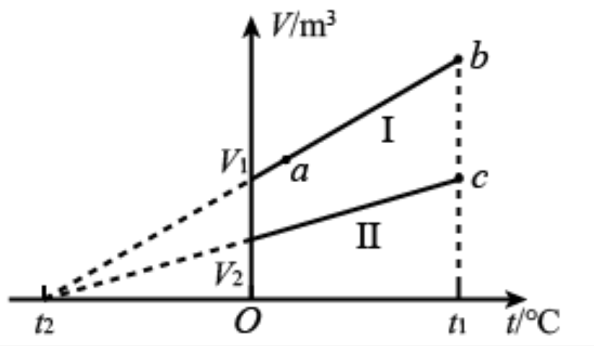
（1）如图，一定量的理想气体经历的两个不同过程，分别由体积-温度（V-t）图上的两条直线I和Ⅱ表示， V ₁和 V ₂分别为两直线与纵轴交点的纵坐标； t ₀为它们的延长线与横轴交点的横坐标， t ₀=-273.15°C； a为直线I上的一点。由图可知，气体在状态 a和 b的压强之比 p _a/ p _b=______;气体在状态 b和 c的压强之比 p _a/ p _c=_________。

（2）如图，一汽缸中由活塞封闭有一定量的理想气体，中间的隔板将气体分为 A、 B两部分；初始时， A、 B的体积均为 V，压强均等于大气压 p ₀。隔板上装有压力传感器和控制装置，当隔板两边压强差超过0.5 p ₀时隔板就会滑动，否则隔板停止运动。气体温度始终保持不变。向右缓慢推动活塞，使 B的体积减小为 V/2。

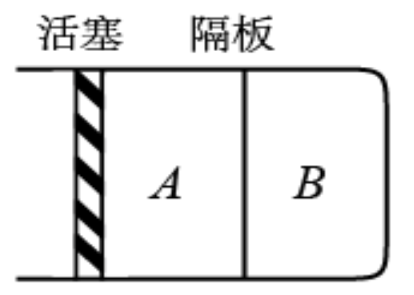
（i）求 A的体积和 B的压强；

（ⅱ）再使活塞向左缓慢回到初始位置，求此时 A的体积和 B的压强。

如图，在直角三角形 $\mathrm{OPN}$ 区域内存在匀强磁场，磁感应强度大小为B、方向垂直于纸面向外。一带正电的粒子从静止开始经电压U加速后，沿平行于x辅的方向射入磁场；一段时间后，该粒子在 $\mathrm{OP}$ 边上某点以垂直于 $x$ 轴的方向射出。已知 $\mathrm{O}$ 点为坐标原点，N点在y轴上， $\mathrm{OP}$ 与 $x$ 轴的夹角为30°，粒子进入磁场的入射点与离开磁场的出射点之间的距离为d，不计重力。求：

（1）带电粒子的比荷；

（2）带电粒子从射入磁场到运动至 $x$ 轴的时间。

（1）如图,一定质量的理型气体从状态a开始,经历过程①、②。③、④到达状态e,对此气体,下列说法正确的是（  ）

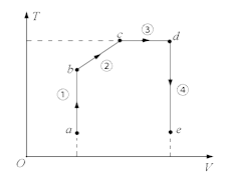
A．	过程①中气体的压强逐渐减小
B．	过程②中气体对外界做正功
C．	过程④中气体从外界吸收了热量
D．	状态c、d的内能相等
E．	状态d的压强比状态b的压强小

（2）如图,容积为V的汽缸由导热材料制成,面积为S的活塞将汽缸分成容积相等的上下两部分,汽缸上部通过细管与装有某种液体的容器相连,细管上有一阀门K。开始时,K关闭,汽缸内上下两部分气体的压强均为P _0,现将K打开,容器内的液体缓慢地流入汽缸,当流入的液体体积为 $\frac{\text{V}}{8}$ 时,将K关闭,活塞平衡时其下方气体的体积减小了 $\frac{\text{v}}{6}$ ·,不计活塞的质量和体积,外界温度保持不变,重力加速度大小为g。求流入汽缸内液体的质量。

（1）关于电磁波，下列说法正确的是（ ）

A．	电磁波在真空中的传播速度与电磁波的频率无关
B．	周期性变化的电场和磁场可以相互激发，形成电磁波
C．	电磁波在真空中自由传播时，其传播方向与电场强度、磁感应强度垂直
D．	利用电磁波传递信号可以实现无线通信，但电磁波不能通过电缆、光缆传输
E．	电磁波可以由电磁振荡产生，若波源的电磁振荡停止，空间的电磁波随即消失

（2）一列简谐横波在介质中沿x轴正向传播，波长不小于10cm．O和A是介质中平衡位置分别位于 $x=0$ 和 $x=5\mathit{cm}$ 处的两个质点． $t=0$ 时开始观测，此时质点O的位移为 $y=4\mathit{cm}$ ，质点A处于波峰位置: $\mathrm{t}=\frac{1}{3}s$ 时，质点O第一次回到平衡位置， $t=1s$ 时，质点A第一次回到平衡位置．求

（i）简谐波的周期、波速和波长；

（ii）质点O的位移随时间变化的关系式．

（1）下列关于能量转换过程的叙述，违背热力学第一定律的有 　　，不违背热力学第一定律、但违背热力学第二定律的有 　　。（填正确答案标号）

A．	$A$ ．汽车通过燃烧汽油获得动力并向空气中散热
B．	$B$ ．冷水倒入保温杯后，冷水和杯子的温度都变得更低
C．	$C$ ．某新型热机工作时将从高温热源吸收的热量全部转化为功，而不产生其他影响
D．	$D$ ．冰箱的制冷机工作时从箱内低温环境中提取热量散发到温度较高的室内

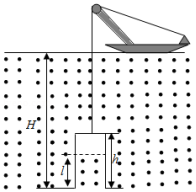
（2）潜水钟是一种水下救生设备，它是一个底部开口、上部封闭的容器，外形与钟相似。潜水钟在水下时其内部上方空间里存有空气，以满足潜水员水下避险的需要。为计算方便，将潜水钟简化为截面积为 $S$ 、高度为 $h$ 、开口向下的圆筒；工作母船将潜水钟由水面上方开口向下吊放至深度为 $H$ 的水下，如图所示。已知水的密度为 $\rho$ ，重力加速度大小为 $g$ ，大气压强为 $p_0$ ， $H>>h$ ，忽略温度的变化和水密度随深度的变化。

$\left(i\right)$ 求进入圆筒内水的高度 $l$ ；

$\left(\mathit{ii}\right)$ 保持 $H$ 不变，压入空气使筒内的水全部排出，求压入的空气在其压强为 $p_0$ 时的体积。

（1）一定量的理想气体从状态a开始，经历等温或等压过程ab、bc、cd、da回到原状态，其P﹣T图象如图所示，其中对角线ac的延长线过原点O．下列判断正确的是（ ）

A．	气体在a、c两状态的体积相等
B．	气体在状态a时的内能大于它在状态c时的内能
C．	在过程cd中气体向外界放出的热量大于外界对气体做的功
D．	在过程da中气体从外界吸收的热量小于气体对外界做的功
E．	在过程bc中外界对气体做的功等于在过程da中气体对外界做的功

（2）一氧气瓶的容积为0.08m ³，开始时瓶中氧气的压强为20个大气压．某实验室每天消耗1个大气压的氧气0.36m ³。当氧气瓶中的压强降低到2个大气压时，需重新充气．若氧气的温度保持不变，求这瓶氧气重新充气前可供该实验室使用多少天？

一细绳跨过悬挂的定滑轮，两端分别系有小球 $A$和 $B$，如图所示。一实验小组用此装置测量小球 $B$运动的加速度。令两小球静止，细绳拉紧，然后释放小球，测得小球 $B$释放时的高度 $h_0=0.590m$，下降一段距离后的高度 $h=0.100m$；由 $h_0$下降至 $h$所用的时间 $T=0.730s$。由此求得小球 $B$加速度的大小为 $a=$　　 $m/s^2$（保留3位有效数字）。从实验室提供的数据得知，小球 $A$、 $B$的质量分别为 $100.0g$和 $150.0g$，当地重力加速度大小为 $g=9.80m/s^2$．根据牛顿第二定律计算可得小球 $B$加速度的大小为 $a\text{'}=$　　 $m/s^2$（保留3位有效数字）。可以看出， $a\text{'}$与 $a$有明显差异，除实验中的偶然误差外，写出一条可能产生这一结果的原因：　　。

如图，在竖直平面内，一半径为R的光滑圆弧轨道ABC和水平轨道PA在A点相切。BC为圆弧轨道的直径。O为圆心，OA和OB之间的夹角为α，sinα= $\frac{3}{5}$ ，一质量为m的小球沿水平轨道向右运动，经A点沿圆弧轨道通过C点，落至水平轨道；在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用，已知小球在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零。重力加速度大小为g。求：

（1）水平恒力的大小和小球到达 C点时速度的大小；    

（2）小球到达 A点时动量的大小；    

（3）小球从 C点落至水平轨道所用的时间。    

一质量为m的烟花弹获得动能E后,从地面竖直升空,当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为E,且均沿竖直方向运动。爆炸时间极短,重力加速度大小为g,不计空气阻力和火药的质量,求    

（1）烟花弹从地面开始上升到弹中火药爆炸所经过的时间.   

（2）爆炸后烟花弹向上运动的部分距地面的最大高度.