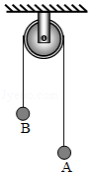
一细绳跨过悬挂的定滑轮，两端分别系有小球 和 ，如图所示。一实验小组用此装置测量小球 运动的加速度。令两小球静止，细绳拉紧，然后释放小球，测得小球 释放时的高度 ，下降一段距离后的高度 ；由 下降至 所用的时间 。由此求得小球 加速度的大小为 （保留3位有效数字）。从实验室提供的数据得知，小球 、 的质量分别为 和 ，当地重力加速度大小为 ．根据牛顿第二定律计算可得小球 加速度的大小为 （保留3位有效数字）。可以看出， 与 有明显差异，除实验中的偶然误差外，写出一条可能产生这一结果的原因： 。
探究：发声的桌面也在振动？
提出问题：
敲桌子时，我们能听到声音，但肉眼却看不见桌子在振动。桌子是否在振动呢？有什么方法证明桌子在发声的同时也在振动呢？
实验设计：
如图2－1所示，在桌子上固定一小块平面镜，让太阳光（或手电筒光、玩具激光发出的激光）照射在平面镜上经平面镜反射后，在墙上出现一个小光斑。
轻轻地敲击桌面，观察墙面上小光斑的位置有什么变化？
用力敲击桌面，观察小光斑位置的变化。
收集证据：
桌面发声时，你发现墙壁上小光斑，这说明。
交流合作：
你认为还有哪些方法可以证明桌子发声时在振动？说说你的办法，试着做一做。
用回声可以帮助船只测量水深，因此在海洋和江河的考察船上都装有声呐。如果声音在水中的传播速度为1500m/s，在考察时发出声音0.8s后接收到了回声，这里的水深为多少？
学校正在开运动会，运动场上你追我赶，精彩纷呈。这时远处的对面传来阵阵鼓声和呐喊声，朝对面看去，总觉得对面的同学敲鼓的动作和听到的鼓声不太协调。
1.小穆不明白，你能解释其中的原因吗？
2.你可以利用你学过的物理知识进行哪些测量？请设计。
粤公网安备 44130202000953号