高中物理力学实验试题

如图1-1所示，A、B分别为单摆做简谐运动时摆球的不同位置.其中，位置A为摆球摆动的最高位置，虚线为过悬点的竖直线.以摆球最低位置为重力势能零点，则摆球在摆动过程中

图1-1
A.位于B处时动能最大
B.位于A处时势能最大
C.在位置A的势能大于在位置B的动能
D.在位置B的机械能大于在位置A的机械能

在“用单摆测定重力加速度”的实验中，用刻度尺测量悬点到小球的距离为96.60 cm，用卡尺量得小球直径是5.260 cm，测量周期有3次，每次是在摆球通过最低点时，按下秒表开始计时，同时将此次通过最低点作为第一次，接着一直数到计时终止，结果如下表.

	1	2	3
数的次数	61	81	71
时间（s）	60.40	79.80	70.60

这个单摆振动周期的测定值是_______________s，当地重力加速度的值是__________m/s².（取三位有效数字）

某同学在“利用单摆测重力加速度”的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间，如图11-4所示，则

图11-4
（1）该摆摆长为 ____________cm，秒表所示读数为____________s.
（2）如果他测得的g值偏小，可能的原因是____________.

A．测摆线长时测了悬线的总长度

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了，使周期变大了

C．开始计时时，秒表过迟按下

D．实验中误将49次全振动数次数记为50次

（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据如图11-5，再以l为横坐标，T²为纵坐标将所得数据连成直线，并求得该直线的斜率为k，则重力加速度g=________________.（用k表示）

图11-5

如图1-8所示，密度为0.8×10³ kg/m³的木球由长l="100" cm的细绳固定在水中，将木球拉离平衡位置一很小角度后释放，水的粘滞阻力不计，木球摆动的周期多大？

图1-8

如图1-5所示，两根长度均为L的细线下端拴一质量为m的小球，两线间夹角为α,今使摆球在垂直纸面的平面内做小幅度振动，求其振动频率.

图1-5

在青岛调准的摆钟,随南极考察船到达南极,这个摆钟

A．变慢了	B．变快了,应减小摆长
C．不变	D．变快了,应加大摆长

如图1-1所示，是一个单摆的共振曲线(取g="10" m/s²)

A．此单摆的摆长约为2.8 m	B．此单摆的周期约为0.3 s
C．若摆长增大，共振曲线的峰将向上移动	D．若摆长增大，共振曲线的峰将向左移动

图1-1

用相同质量的球做一个弹簧振子和一个单摆，它们运动的周期相同，均为T₀.若均换用质量较大(仍相同)的球，设弹簧振子的周期变为T₁，单摆的周期变为T₂，则有

A．T1＞T2,T2＞T0	B．T1＜T0,T2＜T0
C．T1=T0,T2=T0	D．T1＞T0,T2=T0

如图1-7所示，光滑的半球壳半径为R，O点在球心的正下方，一小球由距O点很近的A点由静止放开，同时在O点正上方有一小球自由落下.若运动中阻力不计，为使两球在O点相碰，小球由多高处自由落下(R)?

图1-7

如图1-6所示，摆长为L的单摆，当摆球由A经平衡位置O向右运动的瞬间，另一小球B以速度v同时通过平衡位置向右运动，B与水平面无摩擦，与竖直墙壁碰撞无能量损失.问OC间距离x满足什么条件，才能使B返回时与A球相遇？

图1-6

将在地球上校准的摆钟拿到月球上去，若此钟在月球记录的时间是1 h，那么实际的时间应是______________h(月球表面的重力加速度是地球表面的1/6).若要把此摆钟调准，应使摆长L₀调节为______________.

将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图1-3所示.某同学由此图线提供的信息作出了下列判断:

图1-3
①t="0.2" s时摆球正经过最低点            ②t="1.1" s时摆球正经过最低点
③摆球摆动过程中机械能减小            ④摆球摆动的周期是T="1.4" s
上述判断中,正确的是

A．①③

B．②③

C．③④

D．②④

如图所示，将一根光滑的细金属棒折成V形，顶角为2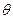，其对称轴竖直，在其中一边套上一个质量为m的小金属环P，
（1）若固定V形细金属棒，小金属环P从距离顶点O为x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O点时需多少时间？
（2）若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动时，则小金属环离对称轴的距离为多少？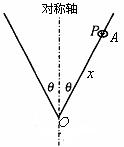

如图，一颗子弹水平射入一原来静止的单摆摆球并留在摆球内，结果单摆开始做简谐运动，其振动图线如图所示。已知子弹的质量为m=10g，摆球质量M=10kg。那么根据力学规律和题中（包括图）提供的信息，对反映振动系统本身性质的物理量、子弹以及子弹和摆球一起运动过程中的守恒量，你能得到那些定量的结果？（g=10m/s²）

如图 10 所示，质量m =" 2kg" 的物体静止在水平地面上，物体与地面间的动摩擦因数μ = 0.75。一个与水平方向成 37°角斜向上、大小F =" 20N" 的力拉物体，

使物体匀加速运动，2s后撤去拉力. 求物体在整个过程中发生的位移？ （sin37°= 0.6，cos37°= 0.8，g =" 10" m/s²）