高中物理力学实验计算题

一质量不计的弹簧原长为10 cm，一端固定于质量m＝2 kg的物体上，另一端施一水平拉力F.（ ，设最大静摩擦力与滑动摩擦力相等）
（1）若物体与水平面间的动摩擦因数为0.2，当弹簧拉长至14cm时，物体恰好被拉动，弹簧的劲度系数多大？
（2）若将弹簧拉长至11 cm时（物体在滑动过程中），物体所受的摩擦力大小为多少？

如图所示，一半径R=1m的圆盘水平放置，在其边缘 E点固定一小桶(可视为质点)。在圆盘直径 DE 的正上方平行放置一水平滑道 BC ，滑道右端 C点 与圆盘圆心O在同一竖直线上，且竖直高度 h =" 1.25" m。AB为一竖直面内的光滑四分之一圆弧轨道，半径r=0.45m，且与水平滑道相切与B点。一质量m=0.2kg的滑块（可视为质点）从A点由静止释放，当滑块经过B点时，圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动，最终物块由C点水平抛出，恰好落入圆盘边缘的小桶内．已知滑块与滑道 BC间的摩擦因数＝0.2。（取g=10m/）

求
（1）滑块到达B点时对轨道的压力
（2）水平滑道 BC的长度；
（3）圆盘转动的角速度ω应满足的条件。

如图所示，在竖直方向上有两个用轻质弹簧相连接的物块，它们的质量分别为m₁、m₂，弹簧的劲度系数分别为k₁、k₂。开始时系统处于静止状态，上面劲度系数为k₁的弹簧处于原长状态。现用竖直向上的力F缓慢的拉动上面弹簧的上端.求质量为m₂的物块刚要离开地面时，上面劲度系数为k₁的弹簧的上端被提起的距离x是多少？

某实验小组进行“用单摆测定重力加速度”的实验,已知单摆在摆动过程中摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t；在测量单摆的摆长为L、摆球的直径为d.
(1)该单摆在摆动过程中的周期为                  .
(2)用上述物理量的符号写出求重力加速度的一般表达式g =                       .
(3)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中的           .

A．单摆的悬点未固定紧,振动中出现松动,使摆线增长了

B．把n次摆动的时间误记为(n + 1)次摆动的时间

C．以摆线长作为摆长来计算

D．以摆线长与摆球的直径之和作为摆长来计算

如图所示，木板A的质量为m="0.1" kg，滑块B的质量为M="0.3" kg，木板A用绳拴住，绳与斜面平行，B恰好能沿倾角为θ=37⁰的斜面在A木板下向下滑动．A、B间以及B与斜面间的动摩擦因数相同都为μ=0.2，sin37⁰=0.6,cos37⁰=0.8，g=10m/s²,求：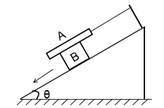

（1）作出B物体受力分析图；
（2）A对B的压力？B对斜面的压力？
（3）B物体所受摩擦力.

额定功率为80kW的汽车在平直公路上行驶，若汽车总质量为2×10³kg，在水平面上行驶时所受的阻力恒为4×10³N。求：
（1）汽车所能达到的最大速度?
（2）若汽车以2m/s²的加速度由静止开始做匀加速直线运动，则匀加速阶段持续多长时间?
（3）汽车起动后第3s末的功率。

如图所示，半径为R=1m的光滑半圆轨道CD竖直放置，与粗糙水平面相切于C点。质量为=10kg的滑块在与水平方向成=37⁰的恒力作用下，从A点由静止开始运动，前进到B点后撤掉力。小物块继续前进经过C点进入半圆轨道，恰能通过最高点D。若恒力大小为100N，且AC段长为10.5m，动摩擦因数为=0.2。求：AB间的距离为多少？（sin37⁰="0.6"   g=10m／s²）

一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为k.设地球的半径为R.假定地球的密度均匀,已知质量均匀分布的球壳对壳内物体的引力为零．求矿井的深度d.

如图所示，两根等高的四分之一光滑圆弧轨道，半径为r、间距为L，图中oa水平，co竖直，在轨道顶端连有一阻值为R的电阻，整个装置处在一竖直向上的匀强磁场中，磁感应强度为B。现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑，到达轨道底端cd时受到轨道的支持力为2mg。整个过程中金属棒与导轨接触良好，轨道电阻不计，求：

(1)金属棒到达轨道底端cd时的速度大小和通过电阻R的电流：
(2)金属棒从ab下滑到cd过程中回路中产生的焦耳热和通过R的电荷量：
(3)若金属棒在拉力作用下，从cd开始以速度v₀向右沿轨道做匀速圆周运动，则在到达ab的过程中拉力做的功为多少?

如图所示，光滑水平面上，一个小球以初速度v向右匀速运动，右侧有一个线长为l的单摆在垂直纸面方向上做小角度振动。摆球的半径为r（不可忽略），其下端在最低点O处恰好与水平面接触，当小球在A点时，摆球恰好处于距离平衡位置最大位移处。若小球与摆球在O点处相撞，小球的体积可忽略，当地重力加速度为g，求：
（1）单摆振动的周期；
（2）AO间的距离。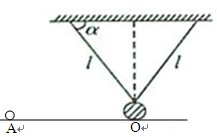

一半径为圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心Ｒ处放一小木块，它与圆盘之间相对静止且随圆盘一起做匀速圆周运动，已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。

（1）求圆盘转动的最大角速度
（2）若圆盘以最大角速度转动，某时刻圆盘突然停止转动，小木块离开圆盘最后落到地面。求木块离开圆盘时的速度及落地点与圆盘中心O的水平距离。

如图所示，物体在15N的推力F的作用下沿水平地面向右匀速直线运动，已知物体的重力为31N，力F与水平方向的夹角为θ=37°，（sin37°=0.6，cos37°=0.8）问：

（1）物体受到地面的支持力为多大
（2）物体受到的摩擦力为多大
（3）物体与地面的动摩擦因数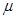

质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动，细绳能承受的最大拉力T_max=46N，转轴离地h=6m，在某次运动中，在最低点时细绳恰好被拉断。（取g=10m/s²）求：

（1）绳断时小球的速度；
（2）绳断后小球在水平方向上的位移。

质量为m=3kg的空木箱，放置在水平地面上，用原长为L₀=12cm的一轻质弹簧沿水平方向施加拉力，当拉力F₁＝8N时，木箱静止；当拉力F₂=9N时，木箱恰能被拉动;当拉力F₃＝7.5N时，木箱恰好做匀速直线运动，此时弹簧的长度L=17cm，(重力加速度g=10m/s²)求：
(1)木箱在8N的拉力作用下受到的摩擦力的大小及木箱与地面间的最大静摩擦力的大小
(2)木箱与地面间的动摩擦因数
(3)弹簧的劲度系数

一根长l=0.625m的细绳，一端栓一质量m=0.4kg的小球，使其在竖直平面内绕绳的另一端做圆周运动，求：
（1）小球通过最高点是的最小速度；
（2）若小球以速度v=3.0m/s通过圆周最高点时，绳对小球的拉力多大？若此时绳突然断了，小球将如何运动？