一半径为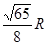 圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心R处放一小木块,它与圆盘之间相对静止且随圆盘一起做匀速圆周运动,已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。
圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心R处放一小木块,它与圆盘之间相对静止且随圆盘一起做匀速圆周运动,已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。
(1)求圆盘转动的最大角速度
(2)若圆盘以最大角速度转动,某时刻圆盘突然停止转动,小木块离开圆盘最后落到地面。求木块离开圆盘时的速度及落地点与圆盘中心O的水平距离。
相关知识点
一半径为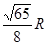 圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心R处放一小木块,它与圆盘之间相对静止且随圆盘一起做匀速圆周运动,已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。
圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心R处放一小木块,它与圆盘之间相对静止且随圆盘一起做匀速圆周运动,已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。
(1)求圆盘转动的最大角速度
(2)若圆盘以最大角速度转动,某时刻圆盘突然停止转动,小木块离开圆盘最后落到地面。求木块离开圆盘时的速度及落地点与圆盘中心O的水平距离。