质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Tmax=46N,转轴离地h=6m,在某次运动中,在最低点时细绳恰好被拉断。(取g=10m/s2)求: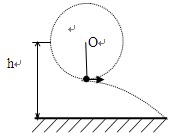
(1)绳断时小球的速度;
(2)绳断后小球在水平方向上的位移。
相关知识点
质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Tmax=46N,转轴离地h=6m,在某次运动中,在最低点时细绳恰好被拉断。(取g=10m/s2)求:
(1)绳断时小球的速度;
(2)绳断后小球在水平方向上的位移。