高中物理力学实验计算题

如图所示，AB为竖直半圆轨道的竖直直径，轨道半径R="0.5" m。轨道A端与水平面相切。光滑小球从水平面以初速度v₀向A滑动，取g="10" m/s²。

(1)若小球经B点时，对轨道的压力恰好为零，求小球落在水平面时到A点的距离。
(2)若小球在B点的速度V_B=4m/s，求小球经A点的瞬间对圆轨道的压力。

如图所示，以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑的地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C两点，一物块（视为质点）被轻放在水平匀速运动的传送带上E点，运动到A点时刚好与传送带速度相同，然后经A点沿半圆轨道滑下，再经B点滑上滑板，滑板运动到C点时被牢固粘连。物块可视为质点，质量为m,滑板质量为M=2m，两半圆半径均为R,板长l=6.5R,板右端到C点的距离L在R<L<5R范围内取值，E点距A点的距离s=5R，物块与传送带、物块与滑板间的动摩擦因数均为，重力加速度g已知。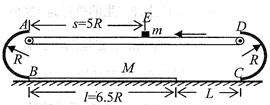

(1)求物块滑到B点的速度大小;
(2)求物块滑到B点时所受半圆轨道的支持力的大小;
(3)试讨论物块从滑上滑板到离开右端的过程中，克服摩擦力做的功与L的关系;并判断物块能否滑到CD轨道的中点。

如图所示，竖直放置的光滑半圆形轨道与动摩擦因数为的水平面AB相切于B点，A、B两点相距L=2.5m，半圆形轨道的最高点为C，现将一质量为m=0.1kg的小球（可视为质点）以初速度v₀=9m/s沿AB轨道弹出，g=10m/s²。求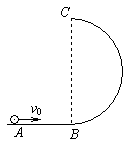

（1）小球到达B点时的速度大小及小球在A、B之间的运动时间；
（2）欲使小球能从最高点C水平抛出，则半圆形轨道的半径应满足怎样的设计要求？
（3）在满足上面（2）设计要求的前提下，半圆形轨道的半径为多大时可以让小球落到水平轨道上时离B点最远？最远距离是多少？

如图所示，一个固定在竖直平面上的光滑半圆形管道，管道里有一个直径略小于管道内径的小球，小球在管道内做圆周运动，从B点脱离后做平抛运动，经过0.3秒后又恰好垂直与倾角为45⁰的斜面相碰到。已知圆轨道半径为R=1m，小球的质量为m=1kg，g取10m/s²。求

（1）小球在斜面上的相碰点C与B点的水平距离
（2）小球经过圆弧轨道的B点时，所受轨道作用力N_B的大小和方向？

一只圆盘绕竖直轴匀速转动，角速度为2 rad/s，质量为2kg的木块随着圆盘一起运动，木块到转轴O的距离为0.3m （）

（1）求此时物体所受摩擦力的大小并说明方向
（2）若将木块到O的距离增大至0.5m，此时木块恰好相对于圆盘不滑动，求木块与圆盘之间的动摩擦因数（设最大静摩擦等于滑动摩擦）

如图所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75mg，求a、b两球落地点间的距离？

 一质量为1kg的木块静止在光滑水平面上，将一个大小为4N的水平恒力作用在该木块上，试求：(g=10m/s²)
（1）恒力作用5s内，恒力所做的功；
（2）恒力作用第5s末，恒力的功率。

半径R=20cm的竖直放置的圆轨道与平直轨道相连接，如图所示。质量m=50g的小球A以一定的初速度由直轨道向左运动，并沿圆轨道的内壁冲上去。如果球A经过N点时速度v₁=4m/s，球A经过轨道最高点M时对轨道的压力为0.5N，取g=10m/s²，求：

（1）小球落地点P与N之间的距离？
（2）小球从N运动到M这一段过程中克服阻力做的功？

、 两种光子的能量之比为2 :1,它们都能使某种金属发生光电效应,且所产生的光电子最大初动能分别为、. 求、两种光子的动量之比和该金属的逸出功.

如图所示，水平虚线下方区域分布着方向水平、垂直纸面向里、磁感应强度为的匀强磁场，整个空间存在匀强电场（图中未画出）。质量为，电荷量为的小球静止于虚线上方点，在某一瞬间受到方向竖直向下、大小为的冲量作用而做匀速直线运动。在点右下方的磁场中有定点，长为l的绝缘轻绳一端固定于点，另一端连接不带点的质量同为的小球，自然下垂。保持轻绳伸直，向右拉起，直到绳与竖直方向有一小于5^。的夹角，在P开始运动的同时自由释放到达点正下方点是速率为。两小球在点发生正碰，碰到电场，磁场消失，两小球黏在一起运动。两小球均视为质点，小球的电荷量保持不变，绳不可伸长不计空气阻力，重力加速度为。

（1）求匀强电场场强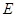的大小和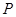进入磁场时的速率；

（2）若绳能承受的最大拉力为,要使绳不断，至少为多大？

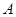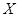（3）求点距虚线的距离

有一辆汽车的质量为2×10³kg，额定功率为9×10⁴W。汽车在平直路面上由静止开始运动，所受阻力恒为3×10³N。在开始起动的一段时间内汽车以1m/s²的加速度匀加速行驶。从开始运动到停止加速所经过的总路程为270m。求：
（1）汽车匀加速运动的时间；
（2）汽车能达到的最大速度；
（3）汽车从开始运动到停止加速所用的时间。

一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为。设地球的半径为。假定地球的密度均匀。已知质量均匀分布的球壳对壳内物体的引力为零，求矿井的深度。

四川某中学物理兴趣小组同学开展研究性学习，对常在火车站看到载重列车启动时，机车首先要倒退的问题进行调查，最后得出结论：因为机车和车厢与铁轨之间的最大静摩擦力大于它们之间的动摩擦力，若机车不倒退直接启动，启动以后机车和车厢与铁轨之间的摩擦力由静摩擦力变为动摩擦力，当列车加速到一定的速度后，列车的机车就必须减少牵引力使列车匀速直线运动，资源不能得到充分的利用，所以载重列车常常采用先倒退的启动方式启动。现假设有一列载重列车，若它不倒退以恒定的牵引力直接启动，机车的牵引力能带动49节车厢（不含机车），那么它利用倒退后用同样大小的恒定牵引力启动，该机车启动59节同样质量的车厢以后，恰好做匀速直线运动，已知机车与各节车厢的质量均为m，机车和各节车厢与铁轨之间的动摩擦力为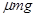，假设机车倒退后，各节车厢之间的挂钩离开相同的距离，机车加速后，每拉动一节车厢的瞬间可近似地认为满足动量守恒定律的条件。求：
（1）每一节车厢与铁轨之间的最大静摩擦力？
（2）列车采用机车倒退的方式启动后做匀速直线运动的速度？（最终结果可以用根式表示）

如图所示，一个上下都与大气相通的直圆筒，内部横截面积为S = 0.01m²，中间用两个活塞A和B封住一定质量的气体。A、B都可沿圆筒无摩擦地上下滑动，且不漏气。A的质量不计，B的质量为M，并与一劲度系数为k = 5×10³ N/m的较长的弹簧相连。已知大气压p₀ = 1×10⁵ Pa，平衡时两活塞之间的距离l₀ =" 0.6" m，现用力压A，使之缓慢向下移动一段距离后，保持平衡。此时用于压A的力F =" 500" N。求活塞A下移的距离。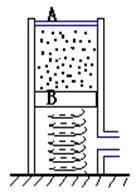

光滑的斜面倾角θ=30º，斜面底端有弹性挡板P，长2l、质量为M的两端开口的圆筒置与斜面上,下端在B点处， PB=2l，圆筒的中点处有一质量为m的活塞，M=m．活塞与圆筒壁紧密接触，最大静摩擦力与滑动摩擦力相等为f=mg/2．每当圆筒中的活塞运动到斜面上AB区间时总受到一个沿斜面向上F=mg的恒力作用，AB=l.现由静止开始从B点处释放圆筒．

（1）求活塞位于AB区间之上和进入AB区间内时活塞的加速度大小；
（2）求圆筒第一次与挡板P碰撞前的速度和经历的时间；
（3）圆筒第一次与挡板P瞬间碰撞后以原速度大小返回，求圆筒沿斜面上升到最高点的时间．