高中物理力学实验计算题

如图所示,斜面小车M静止在光滑水平面上,一边紧贴墙壁.若再在斜面上加一物体m,且M､m相对静止,试分析小车受哪几个力的作用?

如图,人重600  N,木块A重400  N,人与A､A与地面的动摩擦因数均为0.2,现人用水平力拉绳,使他与木块一起向右做匀速直线运动,滑轮摩擦不计,求:

(1)人对绳的拉力;
(2)人脚对A的摩擦力的方向和大小.

如图所示,劲度系数为k₂的轻质弹簧,竖直放在桌面上,上面压一质量为m的物体,另一劲度系数为k₁的轻质弹簧竖直地放在物体上面,其下端与物块上表面连接在一起,要想物体在静止时,下面弹簧承受物重的2/3,应将上面弹簧持上端A竖直向上提高多大的距离?

如图所示,为一轻质弹簧的长度L和弹力F的大小关系图线,试由图线确定:

(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧伸长0.15 m时,弹力的大小.

如图所示,半径为R､内壁光滑的空心圆筒放在地上,将两个重力都是G､半径都是r的球(R<2r<2R)放在圆筒中,求: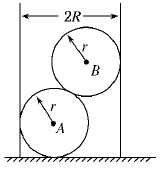

(1)筒底对球A的弹力?
(2)筒壁对球A的弹力是否大于筒壁对球B的弹力?
(3)球A对球B的弹力一定大于重力G吗?
(4)球B对筒壁的压力一定小于重力G吗?

如图所示，一圆锥摆摆长为L，下端拴着质量为m的小球，当绳子与竖直方向成θ角时，绳的拉力大小F是多少？圆锥摆周期T是多少？ （重力加速度为g）

如图4所示，A、B两物体的质量分别为m_A=2.0kg、m_B=4.0kg。 物体A与桌面间的动摩擦因数=0.2，当轻轻释放B后，求：

（1）物体A沿桌面滑行的加速度是多少？
（2）物体A受到绳子的拉力多大？（取g=10m/s²）

如图2－1－16所示，两木块的质量分别为m₁和m₂，两轻质弹簧的劲度系数分别为k₁和k₂，上面木块压在上面的弹簧上(但不拴接)，整个系统处于平衡状态．现缓慢向上提上面的木块，直到它刚离开上面弹簧．在此过程中下面木块移动的距离为多少？

图2－1－16

如图12－1－9甲所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙所示是这个单摆的振动图象．根据图象回答：(取π²＝10)

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s²，试求这个摆的摆长是多少？

如图12－1－6所示，一个光滑的圆弧形槽半径为R，放在水平地面上，圆弧所对的圆心角小于5°.AD的长为x，今有一小球m₁以沿AD方向的初速度v从A点开始运动，要使小球m₁可以与固定在D点的小球m₂相碰撞，那么小球m₁的速度v应满足什么条件？

有人利用安装在气球载人舱内的单摆来确定气球的高度．已知该单摆在海平面处的周期是T₀.当气球停在某一高度时，测得该单摆周期为T.求该气球此时离海平面的高度h.(把地球看做质量均匀分布的半径为R的球体)

(15分)如图11所示，板A的质量为m，滑块B的质量为2m，板A用绳拴住，绳与斜面平行，滑块B沿倾角为α的斜面在A板的中间一段匀速下滑，若A、B之间以及B与斜面间的动摩擦因数相同，求动摩擦因数μ.

(15分)如图10所示，质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上，P、Q之间的动摩擦因数为μ₁，Q与斜面间的动摩擦因数为μ₂(μ₁＞μ₂)．当它们从静止开始沿斜面滑下时，两物体始终保持相对静止，则物体P受到的摩擦力大小为多少？

如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右运动为正方向．图乙是这个单摆的振动图象．根据图象回答：

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s²，这个摆的摆长是多少？

如图所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1.0 kg的物体，物体与斜面间动摩擦因数μ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动，拉力F＝10.0 N，方向平行斜面向上，经时间t₁＝4.0 s绳子突然断了，(sin37°＝0.60，cos37°＝0.80，g＝10 m/s²)求：
 
(1)绳断时物体的速度大小；
(2)从绳子断开到物体再返回到斜面底端的运动时间？