一辆汽车在平直公路上行驶,t=0时汽车从A点由静止开始匀加速直线运动,运动到B点开始刹车做匀减速直线运动直到C点停止.测得每隔2 s的三个时刻物体的瞬时速度记录在下表中,由此可知 ( )
| t/s |
0 |
2 |
4 |
6 |
| v/(m·s-1) |
0 |
8 |
12 |
8 |
A.物体运动过程中的最大速度为12 m/s B.t=3 s的时刻物体恰好经过B点
C.t=10 s的时刻物体恰好停在C点 D.A、B间的距离大于B、C间的距离
如图为一质点运动的位移随时间变化的图象,图象是一条抛物线,方程为x=-5t2+40t,下列说法正确的是( )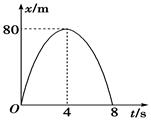
| A.质点的加速度大小是5m/s2 |
| B.质点做匀减速运动,t=8s时质点离出发点最远 |
| C.质点的初速度大小是20m/s |
| D.t=4s时,质点的速度为零 |
一长木板置于粗糙水平地面上,木板左端放置一小物块,在木板右方有一墙壁,木板右端与墙壁的距离为4.5,如图(a)所示。
时刻开始,小物块与木板一起以共同速度向右运动,直至
时木板与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板。已知碰撞后1s时间内小物块的
图线如图(b)所示。木板的质量是小物块质量的15倍,重力加速度大小g取10
。求
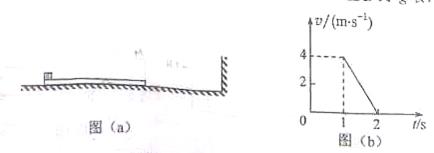
(1)木板与地面间的动摩擦因数及小物块与木板间的动摩擦因数
;
(2)木板的最小长度;
(3)木板右端离墙壁的最终距离。
辨析题:要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1="40" m/s,然后再减速到v2="20" m/s,t1 =  =…;t2 =
=…;t2 =  =…;t= t1 + t2,你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
=…;t= t1 + t2,你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
如图所示,粗糙、绝缘的直轨道固定在水平桌面上,
端与桌面边缘对齐,
是轨道上一点,过
点并垂直于轨道的竖直面右侧有大小
,方向水平向右的匀强电场。带负电的小物体
电荷量是
,质量
,与轨道间动摩擦因数
,
从
点由静止开始向右运动,经过
到达
点,到达
点时速度是
,到达空间
点时速度与竖直方向的夹角为
,且
。
在整个运动过程中始终受到水平向右的某外力
作用,
大小与
的速率
的关系如表所示。
视为质点,电荷量保持不变,忽略空气阻力,取
,求:
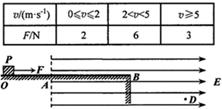
(1)小物体从开始运动至速率为
所用的时间;
(2)小物体从
运动至
的过程,电场力做的功。
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变。用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止.撤去F后,物体开始向左运动,运动的最大距离为4x0。物体与水平面间的动摩擦因数为μ,重力加速度为g。则( )
| A.撤去F后,物体先做匀加速运动,再做匀减速运动 |
B.撤去F后,物体刚运动时的加速度大小为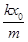 -μg -μg |
C.物体做匀减速运动的时间为2 |
D.物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmg(x0- ) ) |
经检测某车的刹车性能:以标准速度20m/s在平直公路上行驶时,刹车后做匀减速运动10s停下来。某时刻,某车从静止开始,以减速时一半大小的加速度做匀加速直线运动,达到20m/s速度时立即刹车直至停下。求该车从静止开始加速,最后又停下的整个过程中:
(1)该车运动的总时间。
(2)该车前行的总位移。
已知O、A、B、C为同一直线上的四点,AB间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点。已知物体通过AB段与通过BC段所用时间相等。求O与A的距离。
如图所示,在竖直方向上有四条间距均为L=0.5 m的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1 T,方向垂直于纸面向里。现有一矩形线圈abcd,长度ad=3 L,宽度cd=L,质量为0.1 kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向, cd边水平。(g="10" m/s2)则( )
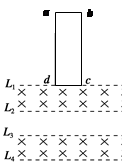
| A.cd边经过磁场边界线L3时通过线圈的电荷量为0. 5 C |
| B.cd边经过磁场边界线L3时的速度大小为4 m/s |
| C.cd边经过磁场边界线L2和 L4的时间间隔为0.25s |
| D.线圈从开始运动到cd边经过磁场边界线L4过程,线圈产生的热量为0.7J |
如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径 ,物块 以 的速度滑入圆轨道,滑过最高点 ,再沿圆轨道滑出后,与直轨道上 处静止的物块 碰撞,碰后粘在一起运动, 点左侧轨道光滑,右侧轨道呈粗糙段、光滑段交替排列,每段长度都为 ,物块与各粗糙段间的动摩擦因数都为 , 、 的质量均为 (重力加速度 取 ; 、 视为质点,碰撞时间极短)。
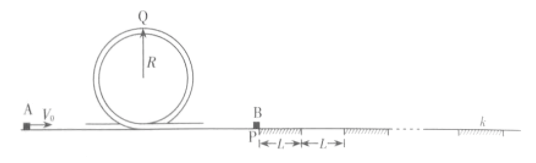
⑴求 滑过Q点时的速度大小 和受到的弹力大小 ;
⑵若碰后 最终停止在第 个粗糙段上,求 的数值;
⑶求碰后
滑至第
个
光滑段上的速度
与
的关系式。
在水平面上有a、b两点,相距20 cm,一质点在一恒定的合外力作用下沿a向b做直线运动,经过0.2 s的时间先后通过a、b两点,则该质点通过a、b中点时的速度大小为 ( )
| A.无论力的方向如何均大于1 m/s |
| B.无论力的方向如何均小于1 m/s |
C.若力的方向由a向b,则大于1 m/s,若力的方向由b向a,则小 于1 m/s 于1 m/s |
D.若力的方向由a向b,则小于1 m/s, 若力的方向由b向a,则大于1 m/s 若力的方向由b向a,则大于1 m/s |
如图,绝缘粗糙的竖直平面左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为
,磁场方向垂直纸面向外,磁感应强度大小为
。一质量为
、电荷量为
的带正电的小滑块从
点由静止开始沿
下滑,到达
点时离开
做曲线运动。
两点间距离为
,重力加速度为
。
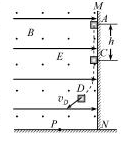
(1)求小滑块运动到点时的速度大小
;(2)求小滑块从
点运动到
点过程中克服摩擦力做的功
;(3)若
点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到
点时撤去磁场,此后小滑块继续运动到水平地面上的
点。已知小滑块在
点时的速度大小为
,从
点运动到
点的时间为
,求小滑块运动到
点时速度的大小vp.
A、B两车在同一直线上向右匀速运动,B车在A车前,A车的速度大小为V1=8m/s, B车的速度大小为V2=20m/s,如图所示。当A、B两车相距x0=28m时,B车因前方突发情况紧急刹车(已知刹车过程的运动可视为匀减速直线运动),加速度大小为a=2m/s2,从此时开始计时,求:
(1)A车追上B车之前,两者相距的最大距离;
(2)A车追上B车所用的时间;
(3)从安全行驶的角度考虑,为避免两车相撞,在题设条件下,A车在B车刹车的同时也应刹车的最小加速度.
如图,质量为
的小车静止在光滑的水平面上,小车AB段是半径为
的四分之一圆弧光滑轨道,
段是长为
的水平粗糙轨道,两段轨道相切于
点,一质量为
的滑块在小车上从
点静止开始沿轨道滑下,重力加速度为
。
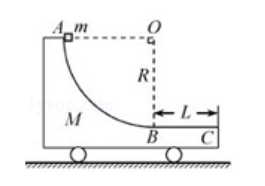
(1)若固定小车,求滑块运动过程中对小车的最大压力;
(2)若不固定小车,滑块仍从
点由静止下滑,然后滑入
轨道,最后从
点滑出小车,已知滑块质量 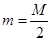 ,在任一时刻滑块相对地面速度的水平分量是小车速度大小的2倍,滑块与轨道
间的动摩擦因数为
,求:
,在任一时刻滑块相对地面速度的水平分量是小车速度大小的2倍,滑块与轨道
间的动摩擦因数为
,求:
① 滑块运动过程中,小车的最大速度
;
② 滑块从
运动过程中,小车的位移大小
。
如图所示,长L=1.5 m、高h=0.45 m、质量M=10 kg的长方体木箱在水平面上向右做直线运动.当木箱的速度v0=3.6 m/s时,对木箱施加一个方向水平向左的恒力F=50 N,并同时将一个质量m=1 kg的小球轻放在木箱上距右端处的P点(小球可视为质点,放在P点时相对于地面间的速度为零),经过一段时间,小球脱离木箱落到地面.已知木箱与地面间的动摩擦因数μ=0.2,而小球与木箱之间的摩擦不计.取g=10 m/s2,求:
(1)小球从开始离开木箱至落到地面所用的时间;
(2)小球放上P点后,木箱向右运动的最大位移;
(3)小球离开木箱时,木箱的速度.