高中物理放射性同位素的应用试题

如图所示，一水平传送带以速度v₁向右匀速传动，某时刻有一物块以水平速度v₂从右端滑上传送带，物块与传送带间的动摩擦因数为μ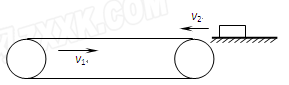

A．如果物块能从左端离开传送带，它在传送带上运动的时间一定比传送带不转动时运动的时间长

B．如果物块还从右端离开传送带，则整个过程中，传送带对物体所做的总功一定不会为正值

C．如果物块还从右端离开传送带，则物体的速度为零时，传送带上产生的滑痕长度达到最长

D．物体在离开传送带之前，可能会做匀速直线运动

(14分)如图(甲)所示，水平放置的平行金属板A、B，两板的中央各有一小孔O₁、O₂，板间距离为d，开关S接1.当t＝0时，在a、b两端加上如图(乙)所示的电压，同时在c、d两端加上如图(丙)所示的电压．此时，一质量为m的带负电微粒P恰好静止于两孔连线的中点处(P、O₁、O₂在同一竖直线上)．重力加速度为g，不计空气阻力．

(1)若在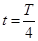时刻将开关S从1扳到2，当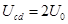时，求微粒P的加速度大小和方向；
(2)若要使微粒P以最大的动能从A板中的O₁小孔射出，问在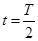到t＝T之间的哪个时刻，把开关S从1扳到2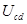，的周期T至少为多少？

水平地面上有一质量为的木块，放在与墙的距离为的位置。现用大小为的水平推力推木块，使木块由静止开始运动，经过的时间到达墙边。
（1）求木块与水平地面间的动摩擦因数；
（2）若仍用大小为的水平力推，为使木块能到达墙边，推力作用的最短时间为多少？
（3）若仍用大小为的力作用，使木块用最短时间到达墙边，则所用时间又为多少？

如图，水平轨道AB与竖直固定圆轨道相切于B点，C为圆轨道最高点，圆轨道半径R=5m．一质量m=60kg的志愿者，驾驶质量M=940kg、额定功率P=40kW的汽   车体验通过圆轨道时所受底座的作用力，汽车从A点由静止以加速度a=2m／s²做匀   加速运动，到达B点时，志愿者调节汽车牵引力，使汽车匀速率通过圆轨道又回到B点，志愿者在C点时所受底座的支持力等于志愿者的重力，已知汽车在水平轨道及圆轨道上的阻力均为汽车对轨道压力的0.1倍，取g=10m／s²，计算中将汽车视为质点。
求：

(1)汽车在C点的速率；
(2)汽车在C点的牵引功率；
(3)AB间的距离及汽车从A点经圆轨道又回到B点的过程所用的时间。

如图所示，一质量m=1kg的小物块(可视为质点)从A点以大小v₀=4m/s的初速度沿切线进入光滑圆轨道AB，经圆弧轨道后滑上与B点等高、静止在粗糙水平面的长木板上，圆弧轨道B端切线水平。已知长木板的质量M=1kg，A、B两点的竖直高度为h=1.0m，AO与BO之间夹角θ=37^O，小物块与长木板之间的动摩擦因数μ₁=0.5，长木板与地面间的动摩擦因数μ₂=0.2，sin37^O=0.6，cos37^O=0.8。求：

（1）小物块运动至B点时的速度v₁大小；
（2）小物块滑动至B点瞬时，对圆弧轨道B点的压力；
（3）长木板至少为多长，才能保证小物块不滑出长木板？
（4）小物块从滑上长木板起到停止运动所经历的时间

一物体做匀减速直线运动，初速度为10m/s，加速度大小为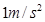，则物体在停止运动前1s内的平均速度为

A．5.5m/s

B．5m/s

C．1m/s

D．0.5m/s

如图所示，有一斜面倾角为θ、质量为M的斜面体置于水平面上，A是最高点，B是最低点，C是AB的中点，其中AC段光滑、CB段粗糙。一质量为m的小滑块由A点静止释放，经过时间t滑至C点，又经过时间t到达B点。斜面体始终处于静止状态，取重力加速度为g，则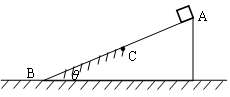

A．A到C与C到B过程中，滑块运动的加速度相同

B．A到C与C到B过程中，滑块运动的平均速度相等

C．C到B过程地面对斜面体的摩擦力水平向右

D．C到B过程地面对斜面体的支持力等于（M+m）g

甲、乙两个同学在直跑道上练习4×100 m接力，他们在奔跑时有相同的最大速度。乙从静止开始全力奔跑需跑出25 m才能达到最大速度，这一过程可看作匀变速直线运动，现在甲持棒以最大速度向乙奔来，乙在接力区伺机全力奔出。若要求乙接棒时奔跑达到最大速度的80%，则：

（1）乙在接力区须奔出多少距离？
（2）乙应在距离甲多远时起跑？

如图所示，相距、质量均为M，两个完全相同木板A、B置于水平地面上，一质量为M、可视为质点的物块C置于木板A的左端。已知物块C与木板A、B之间的动摩擦因数均为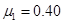，木板A、B与水平地面之间的动摩擦因数为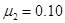，最大静摩擦力可以认为等于滑动摩擦力，开始时，三个物体均处于静止状态。现给物块C施加一个水平方向右的恒力F，且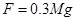，已知木板A、B碰撞后立即粘连在一起。

（1）通过计算说明A与B碰前A与C是一起向右做匀加速直线运动。
（2）求从物块C开始运动到木板A与B相碰所经历的时间。
（3）已知木板A、B的长度均为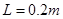，请通过分析计算后判断：物块C最终会不会从木板上掉下来？

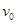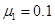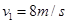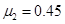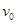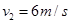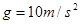如图所示，在冰面上将质量m=1kg的滑块从A点以初速度推出，滑块与冰面的动摩擦因数为，滑块滑行L=18m后到达B点时速度为，现将期间的一段CD用铁刷划擦，使该段的动摩擦因数变为，再使滑块从A以的初速度推出后，到达B点的速度为，取，求：

（1）初速度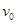的大小；
（2）CD段的长度l；
（3）若AB间用铁刷划擦的CD段的长度不变，要使滑块从A到B的运动时间最长，问铁刷划擦的CD段位于何位置？并求滑块滑行的最长时间（结果保留三位有效数字）。

如图所示，竖直平面坐标系xOy的第一象限，有垂直xOy面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直xOy面向里的水平匀强电场，大小也为E；第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道，轨道最高点与坐标原点O相切，最低点与绝缘光滑水平面相切于N。一质量为m的带电小球从y轴上（y>0）的P点沿x轴正方向进入第一象限后做圆周运动，恰好通过坐标原点O，且水平切入半圆轨道并沿轨道内侧运动，过N点水平进入第四象限，并在电场中运动（已知重力加速度为g）．

（1）判断小球的带电性质并求出其所带电荷量；
（2）P点距坐标原点O至少多高；
（3）若该小球以满足（2）中OP最小值的位置和对应速度进入第一象限，通过N点开始计时，经时间t＝2小球距坐标原点O的距离s为多远？

如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.30m。导轨电阻忽略不计，其间接有固定电阻R=0.40Ω.导轨上停放一质量为m=0.10kg、电阻r=0.20Ω的金属杆ab，整个装置处于磁感应强度B=0.50T的匀强磁场中，磁场方向竖直向下。利用一外力F沿水平方向拉金属杆ab，使之由静止开始做匀加速直线运动，电压传感器可将R两端的电压U即时采集并输入电脑，并获得U随时间t的关系如图乙所示。求：

（1）金属杆加速度的大小；
（2）第2s末外力的瞬时功率。

如图所示的传送带，其水平部分ａｂ的长度为２ｍ，倾斜部分ｂｃ的长度为４ｍ，ｂｃ与水平面的夹角为θ=37⁰，将一小物块A（可视为质点）轻轻放于a端的传送带上，物块A与传送带间的动摩擦因数为μ=0.25.传送带沿图示方向以v=2m/s的速度匀速运动，若物块A始终未脱离皮带（g=10m/s²，sin37⁰=0.6，cos37⁰=0.8）。求：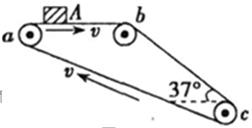

（1）小物块从a端被传送到b端所用的时间
（2）小物块被传送到c端时的速度大小
（3）若当小物块到达b端时，传送到的速度突然增大为v＇，问v＇的大小满足什么条件可以使小物块在传送带bc上运动所用的时间最短？

如图，可看作质点的小物块放在长木板正中间，已知长木板质量为M=4kg，长度为L=2m，小物块质量为m=1kg，长木板置于光滑水平地面上，两物体皆静止。现在用一大小为F的水平恒力作用于小物块上，发现只有当F超过2.5N时，才能让两物体间产生相对滑动。设两物体间的最大静摩擦力大小等于滑动摩擦力大小，重力加速度g=10m/s²，试求：

（1）小物块和长木板间的动摩擦因数。
（2）若一开始力F就作用在长木板上，且F=12N，则小物块经过多长时间从长木板上掉下？

如图，是某一工厂加工、检验工件过程的简化图。与水平面成θ=25^o角的倾斜的绷紧传送带（为传送区），AB长为S=6m，在电动机带动下，始终以v₀=m/s顺时针匀速转动；台面BC（为检验区，若加工合格将被取走，不合格继续保留重新加工）与传送带平滑连接于B点，BC长L=2.2m；半圆形光滑轨道（为加工区）半径R=1.0m，与水平台面相切于C点。一个质量为m=0.1kg的待加工小工件（可以视为质点），从A点无初速释放，小工件与传送带的动摩擦因数μ₁ =0.5，小工件与台面的动摩擦因数μ₂ =0.01。（注意：本题不考虑加工与检验过程对工件运动造成的影响；小工件能够以相同速率在台面与传送带间的B点相互平稳滑动；已知sin25^o=0.4；cos25^o=0.9；重力加速度取g=10m/s²）求：

（1）小工件从A点第一次运动到B点所用的时间；
（2）小工件最多可以进入检验区几次和进入加工区几次，若始终不合格的小工件最后停留在何处；
（3）若小工件从A点无初速释放，经过两次加工合格，因传送工件电动机要多消耗多少的电能。（本小题计算中，取，）