一质点自x轴原点O出发，沿正方向以加速度a运动，经过to时间速度变为v0，接着以–a加速度运动，当速度变为–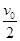
时，加速度又变为a，直至速度变为
时，加速度再变为–a，直至速度变为–
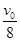……，其v-t图象如图所示，则下列说法中正确的是（ ）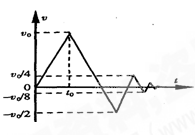
| A．质点一直沿x轴正方向运动； |
| B．质点将在x轴上一直运动，永远不会停止； |
| C．质点最终静止时离开原点的距离一定大于voto； |
| D．质点运动过程中离原点的最大距离为voto。 |
如图所示，一平直的传送带以速度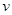
=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m．从A处把工件无初速地放到传送带上，经过时间
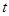=6s能传送到B处．求：
（1）上述过程中工件在传送带上做匀加速运动的时间。
（2）若皮带速度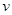可取不同值，求出工件从A至B的时间随皮带运动速度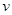的变化的函数关系式。
如图所示，质量为m的物体在水平传送带上由静止释放，传送带由电动机带动，始终保持以速度v匀速运动，物体与传送带间的动摩擦因数为μ，物体过一会儿能保持与传送带相对静止，对于物体从静止释放到相对静止这一过程，下列说法正确的是
| A．电动机多做的功为 mv2/2 |
| B．物体在传送带上的划痕长v2 /2μg |
| C．传送带克服摩擦力做的功为mv2 /2 |
| D．电动机增加的功率为μmgv |
如图，表面光滑的固定斜面顶端安装一定滑轮，小物块A、B用轻绳连接并跨过滑轮（不计滑轮的质量和摩擦）．初始时刻，A、B处于同一高度并恰好处于静止状态．剪断轻绳后A下落、B沿斜面下滑，则从剪断轻绳到物块着地，两物块
A、速度的变化量相同 B、机械能的变化量相同
C、落地时间相同 D、重力做功的平均功率相同
如图所示，两平行金属导轨轨道MN、MʹNʹ间距为L，其中MO和MʹOʹ段与金属杆间的动摩擦因数μ＝0．4，ON和OʹNʹ段光滑且足够长，两轨道的交接处由很小的圆弧平滑连接，导轨电阻不计，左侧接一阻值为R的电阻和电流传感器，轨道平面与水平面的夹角分别为α＝53°和β＝37°。区域PQPʹQʹ内存在垂直轨道平面向下的有界匀强磁场，磁场宽度为d，PPʹ的高度为h2＝0．3m，。现开启电流传感器，同时让质量为m、电阻为r的金属杆ab自高h1＝1．5m处由静止释放，金属杆与导轨垂直且保持接触良好，电流传感器测得初始一段时间内的I t（电流与时间关系）图象如图乙所示（图中I0为已知）。求：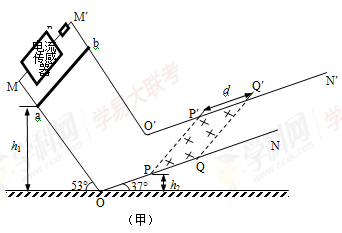
（1）金属杆第一次进入磁场区域时的速度大小v1（重力加速度为g取10m/s2）；
（2）匀强磁场的磁感应强度B和金属杆第二次进入磁场区域时的速度大小（此后重力加速度取g）；
（3）电阻R在t1 t3时间内产生的总热能QR（用v1和其它已知条件表示）。
货车A正在该公路上以20m/s的速度匀速行驶，因疲劳驾驶司机注意力不集中，当司机发现正前方有一辆静止的轿车B时，两车距离仅有64m。
（1）若此时B车立即以2m/s2的加速度启动，通过计算判断：如果A车司机没有刹车，是否会撞上B车；若不相撞，求两车相距最近时的距离；若相撞，求出从A车发现B车开始到撞上B车的时间.
（2）若A车司机发现B车，立即刹车（不计反应时间）做匀减速直线运动，加速度大小为2m/s2（两车均视为质点），为避免碰撞，在A车刹车的同时， B车立即做匀加速直线运动（不计反应时间），问：B车加速度a2至少多大才能避免事故.（这段公路很窄，无法靠边让道）
如图所示，半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点，O为圆弧圆心，D为圆弧最低点．斜面体ABC固定在地面上，顶端B安装一定滑轮，一轻质软细绳跨过定滑轮（不计滑轮摩擦）分别连接小物块P、Q （两边细绳分别与对应斜面平行），并保持P、Q两物块静止．若PC间距为L1=0.25m，斜面MN足够长，物块P质量m1= 3kg，与MN间的动摩擦因数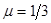
，求：（sin37°=0.6，cos37°=0.8）
（1）烧断细绳后，物块P第一次到达D点时对轨道的压力大小；
（2）物块P第一次过M点后0.3s到达K点，则 MK间距多大；
（3）物块P在MN斜面上滑行的总路程．
一观察者站在第一节车厢前端，当列车从静止开始做匀加速运动时
A．每节车厢末端经过观察者的速度之比是1∶ ∶ ∶…∶ |
| B．每节车厢末端经过观察者的时间之比是1∶3∶5∶…∶n |
| C．在相等时间里经过观察者的车厢数之比是1∶3∶5∶… |
| D．在相等时间里经过观察者的车厢数之比是1∶2∶3∶… |
(11分)如图光滑水平导轨AB的左端有一压缩的弹簧，弹簧左端固定，右端前放一个质量为m=1kg的物块（可视为质点），物块与弹簧不粘连，B点与水平传送带的左端刚好平齐接触，传送带的长度BC的长为L=6m，沿逆时针方向以恒定速度v=2m/s匀速转动。CD为光滑的水平轨道，C点与传送带的右端刚好平齐接触，DE是竖直放置的半径为R=0.4m的光滑半圆轨道，DE与CD相切于D点。已知物块与传送带间的动摩擦因数μ=0.2，取g=10m/s2。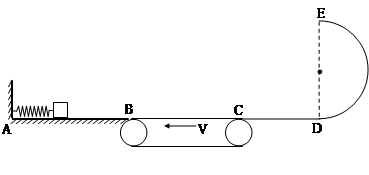
（1）若释放弹簧，物块离开弹簧，滑上传送带刚好能到达C点，求弹簧储存的弹性势能Ep；
（2）若释放弹簧，物块离开弹簧，滑上传送带能够通过C点，并经过圆弧轨道DE，从其最高点E飞出，最终落在CD上距D点的距离为x=1.2m处（CD长大于1.2m），求物块通过E点时受到的压力大小；
（3）满足（2）条件时，求物块通过传送带的过程中产生的热能。
如图所示，绷紧的传送带与水平面的夹角θ=30°，皮带在电动机的带动下，始终保持v0=2m/s的速率运行．现把一质量m=10kg的工件（可看做质点）轻轻放在皮带的底端，经时间t=1.9s，工件被传送到h=1.5m的高处，取g=10m/s2．求：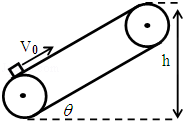
（1）工件与皮带间的动摩擦因数；
（2）电动机由于传送工件多消耗的电能．
如图甲所示是一打桩机的简易模型.质量m=1kg的物体在恒定拉力F作用下从与钉子接触处由静止开始运动，上升一段高度后撤去F，到最高点后自由下落，撞击钉子，将钉子打入一定深度.物体上升过程中，机械能E与上升高度h的关系图像如图乙所示.不计所有摩擦，g取10m/s2.求：
（1）物体上升到1m高度处的速度；
（2）物体上升1 m后再经多长时间才撞击钉子（结果可保留根号）；
（3）物体上升到0.25m高度处拉力F的瞬时功率.
如图所示，竖直平面内，一带正电的小球，系于长为L的不可伸长的轻线一端，线的另一端固定为O点，它们处在匀强电场中，电场的方向水平向右，场强的大小为E．已知电场对小球的作用力的大小等于小球的重力．现先把小球拉到图中的P1处，使轻线伸直，并与场强方向平行，然后由静止释放小球．已知小球在经过最低点的瞬间，因受线的拉力作用，其速度的竖直分量突变为零，水平分量没有变化，（不计空气阻力）则小球到达与P1点等高的P2点时线上张力T为多少（ ）
| A．mg | B．3mg | C．4mg | D．5mg |
一弹簧秤的秤盘A的质量m＝1.5kg，盘上放一物体B，B的质量为M＝10.5kg，弹簧本身质量不计，其劲度系数k＝800N/m，系统静止时如图所示。现给B一个竖直向上的力F使它从静止开始向上做匀加速运动，已知在头0.20s内，F是变力，以后F是恒力，求F的最大值和最小值。(g取10m/s2)
在水平长直的轨道上，有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动．某时刻将一质量为m的小滑块轻放到车面的中点，滑块与车面间的动摩擦因数为μ．
（1）证明：若滑块最终停在小车上，滑块和车摩擦产生的内能与动摩擦因数μ无关，是一个定值．
（2）已知滑块与车面间动摩擦因数μ=0.2，滑块质量m=1kg，车长L=2m，车速v0=4m/s，取g=10m/s2，当滑块放到车面中点的同时对该滑块施加一个与车运动方向相同的恒力F，要保证滑块不能从车的左端掉下，恒力F大小应该满足什么条件？
（3）在（2）的情况下，力F取最小值，要保证滑块不从车上掉下，力F的作用时间应该在什么范围内？
钓鱼岛是我国固有领土，决不允许别国侵占。近期，我人民海军为此进行登陆演练，假设一艘战舰因吨位大吃水太深，只能停锚在离海岸登陆点较远处。登陆队员需要从较高的军舰甲板上，利用绳索下滑到登陆快艇上再行登陆，若绳索两端固定好后，与竖直方向的夹角θ=45°。队员下滑时改变特殊手套（握力足够大时才有摩擦力）在绳索上的握力大小以调整下滑加速度大小，恰好保证了全程加速度大小相等，假定做先匀加速运动后立即匀减速运动，登上快艇时速度为刚好零。为了安全，绳索上只能容一人滑动，每人按要求丢下随身携带的石头使其自由下落，第1名队员下滑时丢下自己的石头，从第二名队员开始听到前一队员丢下石头的击水声就丢下自己的石头，当听到自己石头的击水声时立即下滑，同时再丢第二块石头（忽略声音传播时间），这样恰好保证了绳上只有一人下滑，10名队员在40s内恰好全部登上快艇。重力加速度g=10m/s2，求：
（1）军舰甲板与快艇的高度差H。
（2）下滑时加速度大小a。
（3）某队员连同装备在内质量为m=200kg，在加速下滑过程中他对绳的作用力大小F。
粤公网安备 44130202000953号