如图所示,MN为裸金属杆,在重力的作用下,贴着竖直平面内的光滑金属长直导轨下滑,导轨的间距 ,导轨的上端接有
,导轨的上端接有 的电阻,导轨和金属杆的电阻不计,整个装置处于
的电阻,导轨和金属杆的电阻不计,整个装置处于 的水平匀强磁场中,当杆稳定匀速下落时,每秒有0.02J的重力势能转化为电能,则这时MN杆的下落速度v的大小等于多少?
的水平匀强磁场中,当杆稳定匀速下落时,每秒有0.02J的重力势能转化为电能,则这时MN杆的下落速度v的大小等于多少?
如图甲所示,有一面积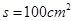 ,匝数n=100匝的闭合线圈,电阻为
,匝数n=100匝的闭合线圈,电阻为 ,线圈中磁场变化规律如图乙所示,磁场方向垂直纸面向里为正方向,求:
,线圈中磁场变化规律如图乙所示,磁场方向垂直纸面向里为正方向,求: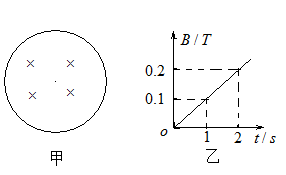
(1)t=1s时,穿过每匝线圈的磁通量为多少?
(2)t=2s内,线圈产生的感应电动势为多少?
如图所示,两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上,导轨间距为L,电阻忽略不计且足够长,以宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B.另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形线框连在一起组成的固定装置,总质量为m,导体棒中通有大小恒为I的电流.将整个装置置于导轨上,开始时导体棒恰好位于磁场的下边界处.由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度为g.
(1)求刚释放时装置加速度的大小;
(2)求这一过程中线框中产生的热量;
(3)之后装置将向下运动,然后再向上运动,经过若干次往返后,最终整个装置将在斜面上作稳定的往复运动.求稳定后装置运动的最高位置与最低位置之间的距离.
如图甲所示,质量m=6.0×10-3 kg、边长L=0.20 m、电阻R=1.0 Ω的正方形单匝金属线框abcd,置于倾角α=30°的绝缘斜面上,ab边沿水平方向,线框的上半部分处在垂直斜面向上的匀强磁场中,磁感应强度B随时间t按图乙所示的规律周期性变化,若线框在斜面上始终保持静止,取g=10 m/s2.试求:
(1)在0~2.0 ×10-2 s时间内线框中产生的感应电流的大小;
(2)在t =1.0×10-2 s时线框受到斜面的摩擦力;
水平放置的两根平行金属导轨ad和bc,导轨两端a、b和c、d两点分别连接电阻R1和R2,组成矩形线框,如图所示,ad和bc相距L=0.5m,放在竖直向下的匀强磁场中,磁感应强度为B=1T,一根电阻为0.2Ω的导体棒PQ跨接在两根金属导轨上,在外力作用下以4m/s的速度,向右匀速运动,如果电阻R1=0.3Ω,R2=0.6Ω,导轨ad和bc的电阻不计,导体与导轨接触良好.求:
(1)导体棒PQ中产生的感应电流的大小;
(2)导体棒PQ上感应电流的方向;
(3)导体棒PQ向右匀速滑动的过程中,外力做功的功率.
如图所示,“ ”型平行金属导轨,倾角
”型平行金属导轨,倾角 =370,导体棒MN、PQ分别与导轨垂直放置,质量分别为m1和m2,MN与导轨的动摩擦因数
=370,导体棒MN、PQ分别与导轨垂直放置,质量分别为m1和m2,MN与导轨的动摩擦因数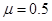 ,PQ与导轨无摩擦,设最大静摩擦力等于滑动摩擦力,装置整体置于方向垂直倾斜导轨平面向上的匀强磁场中,现将导体棒PQ由静止释放(设PQ离底端足够远)。试分析m1与m2应该满足什么关系,才能使导体棒MN在导轨上运动。
,PQ与导轨无摩擦,设最大静摩擦力等于滑动摩擦力,装置整体置于方向垂直倾斜导轨平面向上的匀强磁场中,现将导体棒PQ由静止释放(设PQ离底端足够远)。试分析m1与m2应该满足什么关系,才能使导体棒MN在导轨上运动。
一平行金属导轨水平面内固定,导轨间距L=0.5m,导轨右端接有电阻RL=4 小灯泡,导轨电阻不计,如图甲。在导轨的MNQP矩形区域内有竖直向上的磁场,MN、PQ间距d=3m,此区域磁感应强度B随时间t变化规律如图乙所示,垂直导轨跨接一质量m=1kg的金属杆,其电阻r=1
小灯泡,导轨电阻不计,如图甲。在导轨的MNQP矩形区域内有竖直向上的磁场,MN、PQ间距d=3m,此区域磁感应强度B随时间t变化规律如图乙所示,垂直导轨跨接一质量m=1kg的金属杆,其电阻r=1 ,金属杆与导轨间的动摩擦因数为
,金属杆与导轨间的动摩擦因数为 =0.2,在t=0时刻,给金属棒以速度v0=2m/s,同时施加一向右的外力F,使其从GH处向右运动,在0--2s内小灯发光亮度始终没变化,求:
=0.2,在t=0时刻,给金属棒以速度v0=2m/s,同时施加一向右的外力F,使其从GH处向右运动,在0--2s内小灯发光亮度始终没变化,求:
(1)通过计算分析2s内金属杆的运动情况;
(2)计算2s内外力F的大小;
(3)计算2s内整个系统产生热量。
如图所示,一水平放置的平行导体框架宽度L=0.5m,接有电阻R=0.20Ω,磁感应强度B=0.40T的匀强磁场垂直导轨平面方向向下,仅有一导体棒ab跨放在框架上,并能无摩擦地沿框架滑动,框架及导体ab电阻不计,当ab以v=4.0m/s的速度向右匀速滑动时.试求:
(1)导体ab上的感应电动势的大小.
(2)要维持ab向右匀速运行,作用在ab上的水平力为多大?
(3)电阻R上产生的焦耳热功率为多大?
如图所示,在高度为L、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B.质量为m、边长为L、电阻为R的正方形导线框abcd,在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g,不计空气阻力,求:
(1)导线框刚下落时,bc边距磁场上边界MN的高度h;
(2)导线框离开磁场的过程中,通过导线框某一横截面的电量q;
(3)导线框穿越磁场的整个过程中,导线框中产生的热量Q.
南昌二中第46届田径运动会于2015年10月23日胜利召开。在运动会开幕式上,一航拍直升机悬停在学校操场上空某处。该处地磁场的磁感应强度沿竖直方向的分量为B,直升机金属螺旋桨叶片长为L,螺旋桨转动的频率为f,站在地面向上看,螺旋桨作顺时针方向转动。螺旋桨叶片的近轴端为a,远轴端为b,如图所示。如果忽略a到转轴中心线的距离,求每个叶片在转动过程中产生的电动势E,并指出a、b两点哪一端电势较高。
如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面夹角θ=30°,导轨电阻不计.磁感应强度为B=2T的匀强磁场垂直导轨平面向上,长为L=0.5m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨电接触良好,金属棒ab的质量m=1kg、电阻r=1Ω.两金属导轨的上端连接右端电路,灯泡电阻RL=4Ω,定值电阻R1=2Ω,电阻箱电阻R2=12Ω,重力加速度为g=10m/s2,现闭合开关,将金属棒由静止释放,下滑距离为s0=50m时速度恰达到最大,试求:
(1)金属棒下滑的最大速度vm;
(2)金属棒由静止开始下滑2s0的过程中整个电路产生的电热Q.
如图所示,在水平面内固定着足够长且光滑的平行金属轨道,轨道间距L=0.40m,轨道左侧连接一定值电阻R=0.80Ω。将一金属直导线ab垂直放置在轨道上形成闭合回路,导线ab的质量m=0.10kg、电阻r=0.20Ω,回路中其余电阻不计。整个电路处在磁感应强度B=0.50T的匀强磁场中,B的方向与轨道平面垂直。导线ab在水平向右的拉力F作用下,沿力的方向以加速度a=2.0m/s2由静止开始做匀加速直线运动,求:
(1)5s末的感应电动势大小;
(2)5s末通过R电流的大小和方向;
(3)5s末,作用在ab金属杆上的水平拉力F的大小。
如图甲所示,两根足够长的平行光滑金属导轨MN、PQ被固定在水平面上,导轨间距 L="0.6" m,两导轨的左端用导线连接电阻R1 及理想电压表 ,电阻为r="2" Ω的金属棒垂直于导轨静止在AB处;右端用导线连接电阻R2,已知R1=2Ω,R2=1Ω,导轨及导线电阻均不计.在矩形区域CDEF内有竖直向上的磁场,CE="0.2" m,磁感应强度随时间的变化如图乙所示.t=0.2s后的某一时刻对金属棒施加一水平向右的恒力,使金属棒能够刚进入磁场的速度为2m/s,并能在磁场中保持匀速直线运动。求
,电阻为r="2" Ω的金属棒垂直于导轨静止在AB处;右端用导线连接电阻R2,已知R1=2Ω,R2=1Ω,导轨及导线电阻均不计.在矩形区域CDEF内有竖直向上的磁场,CE="0.2" m,磁感应强度随时间的变化如图乙所示.t=0.2s后的某一时刻对金属棒施加一水平向右的恒力,使金属棒能够刚进入磁场的速度为2m/s,并能在磁场中保持匀速直线运动。求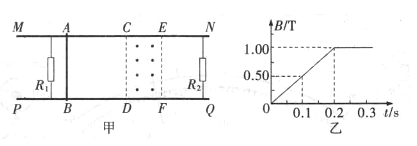
(1)t="0.1" s时电路中的感应电动势
(2)从t=0时刻到金属棒运动出磁场过程中整个电路产生的热量.
如图所示,一U形金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5T,AC以8m/s的速度水平向右移动,电阻R为5Ω,(其它电阻均不计)。
(1)计算感应电动势的大小;
(2)求出电阻R中的电流有多大。