如图所示,粗细均匀的玻璃细管上端封闭,下端开口,竖直插在大而深的水银槽中,管内封闭有一定质量的空气,玻璃细管足够长,管内气柱长4 cm,管内外水银面高度差为10 cm。现将玻璃管沿竖直方向缓慢移动. (大气压强相当于75cmHg)求:
①若要使管内外水银面恰好相平,此时管内气柱的长度;
②若要使管内外水银面高度差为15 cm,玻璃管又应如何移动多少距离。
如图所示,在固定的气缸A和B中分别用活塞封闭一定质量的理想气体,活塞面积之比为SA:SB = 1:2。两活塞以穿过B的底部的刚性细杆相连,可沿水平方向无摩擦滑动。两个气缸都不漏气。初始时,A、B中气体的体积皆为V0,温度皆为T0="300" K。A中气体压强pA=1.5p0,p0是气缸外的大气压强。现对A加热,使其中气体的压强升到 pA = 2.0p0,同时保持B中气体的温度不变。求此时A中气体温度TA’。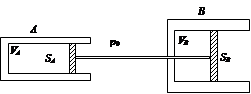
如图所示,水平放置的 A、B 是两个相同气缸,其长度和截面积分别为20 cm和10 cm2,C 是可在气缸内无摩擦滑动的、厚度不计的活塞,D为阀门,整个装置均由导热良好材料制成.开始阀门关闭,A 内有压强为 pA = 2.0×105 Pa 的氮气,B 内有压强为pB = 1.2×105 Pa的氧气;阀门打开后,活塞 C开始移动,最后达到平衡.试求活塞 C 移动的距离及平衡后 B 中气体的压强.假设环境温度始终不变.
如图所示,地面上有一质量M="10" kg的圆形汽缸,缸内横截面积S ="0.01" m2,汽缸内有用一轻活塞封闭着一定质量的理想气体。一上端固定、劲度系数k=1000N/m的轻弹簧下端与活塞相连,弹簧自然长时,活塞离汽缸底部的距离l1="0.5" m,气体温度T1=500K。已知大气压强p0=l×105Pa,不计活塞与汽缸壁间的摩擦,取g="10" m/s2 
①当温度降低到多少时,汽缸对地面恰好没有压力?
②若缓慢降温至270 K时,汽缸将离开地面上升多高?
(1)下列说法正确的是 。
| A.同种物质不可能以晶体或非晶体两种形态出现 |
| B.冰融化为同温度的水时,分子势能增加 |
| C.分子间引力随距离增大而减小,而斥力随距离增大而增大 |
| D.大量分子做无规则运动的速率有大有小,所以分子速率分布没有规律 |
(2)已知二氧化碳摩尔质量为M ,阿伏加德罗常数为N A,在海面处容器内二氧化碳气体的密度为ρ。现有该状态下体积为V 的二氧化碳,则含有的分子数为 。实验表明,在2500m深海中,二氧化碳浓缩成近似固体的硬胶体。将二氧化碳分子看作直径为D的球,则该容器内二氧化碳气体全部变成硬胶体后体积约为 。
(3)如图,一定质量的理想气体从状态A 变化到状态B ,内能增加了10J。已知该气体在状态A 时的体积为1.0×l0 -3 m3。求: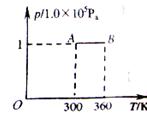
①该气体在状态B 时的体积;
②该气体从状态A 到状态B 的过程中,气体与外界传递的热量。
如图所示,内径均匀的直角细玻璃管ABC两端开口,AB段竖直,BC段水平,AB=100cm,BC=40cm,在水平段BC内有一长10cm的水银柱,其左端距B点10cm,环境温度为330 K时,保持BC段水平,将玻璃管A端缓慢竖直向下插入大水银槽中,使A端在水银面下10cm。已知大气压为75cmHg且保持不变,若环境温度缓慢升高,求温度升高到多少K时,水银柱刚好全部溢出。
如图所示,一环形玻璃管放在水平面内,管内封闭有一定质量的理想气体,一固定的活塞C和一能自由移动的活塞A将管内的气体分成体积相等的两部分Ⅰ、Ⅱ。现保持气体Ⅱ的温度不变仍为T0 =300K,对气体Ⅰ缓慢加热至T=500K,求此时气体Ⅰ、Ⅱ的体积之比。(活塞绝热且不计体积)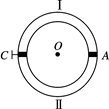
两端开口、内表面光滑的U形管处于竖直平面内,如图所示,质量均为m="10" kg的活塞A、B在外力作用下静止于左右管中同一高度A处,将管内空气封闭,此时管内外空气的压强均为p0=1.0×105 Pa左管和水平管横截面积S1="10" cm2,右管横截面积S2="20" cm2,水平管长为3h。现撤去外力让活塞在管中下降,求两活塞稳定后所处的高度。(活塞厚度均大于水平管直径,管内气体初末状态温度相同,g取10 m/s2)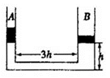
如图所示,用销钉固定的光滑绝热活塞把水平放置的绝热气缸分隔成容积相同的A、B两部分,A、B缸内分别封闭有一定质量的理想气体。初始时,两部分气体温度都为t0=27℃,A部分气体压强为pA0=2×105Pa,B部分气体压强为pB0=1×105Pa。拔去销钉后,保持A部分气体温度不变,同时对B部分气体加热,直到B内气体温度上升为t=127℃,停止加热,待活塞重新稳定后,(活塞厚度可忽略不计,整个过程无漏气发生)求: 
(1)A部分气体体积与初始体积之比VA:VA0;
(2)B部分气体的压强pB。
一定质量的理想气体体积V与热力学温度T的关系图象如图所示,气体在状态A时的压强P0=1.0×105 Pa,线段AB与V轴平行。
(1)求状态B时的压强为多大?
(2)气体从状态A变化到状态B过程中,对外界做的功为10 J,求该过程中气体吸收的热量为多少?
如图所示,一导热性能良好、内壁光滑的气缸竖直放置,在距气缸底部l=36cm处有一与气缸固定连接的卡环,活塞与气缸底部之间封闭了一定质量的气体.当气体的温度T0=300K、大气压强p0=1.0×105Pa时,活塞与气缸底部之间的距离l0=30cm,不计活塞的质量和厚度.现对气缸加热,使活塞缓慢上升,求:
①活塞刚到卡环处时封闭气体的温度T1.
②封闭气体温度升高到T2=540K时的压强p2.
如图所示,在一圆形管道内封闭有理想气体,用一固定活塞K和不计质量可自由移动的活塞A,将管内气体分割成体积相等的两部分。固定活塞K、可动活塞A和管道中心O处于同一水平线上。管道内气体温度都为T0=300K,压强都为P0=1.0×105Pa。现保持管道下部分气体温度不变,只对管道上部分气体缓慢加热,当可动活塞P缓慢移动到管道最低点时(不计摩擦),求;
①下部分气体的压强;
②上部分气体的温度。
(1)下列说法正确的是(选对一个给2分,选对两个给4分,选对三个给6分,选错一个扣3分,最低得分为0分)
| A.布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动 |
| B.只要知道水的摩尔质量和一个水分子的质量,就可以计算出阿伏加德罗常数 |
| C.在使两个分子间的距离由很远(r >10–9 m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大 |
| D.通过科技创新,我们能够研制出内能全部转化为机械能的热机 |
E.内能不同的物体,它们分子热运动的平均动能可能相同
(2)在粗测油酸分子大小的实验中,具体操作如下:
①取纯油酸1.00mL注入容量为250mL的瓶内,然后向瓶中加入酒精,直到液面达到250mL的刻度为止,摇动瓶使油酸在酒精中充分溶解,形成油酸的酒精溶液;
②用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数直到量筒达到1.00mL为止,恰好共滴了100滴;
③在浅盘内注入约2cm深的水,将痱子粉均匀撒在水面上,再用滴管吸取油酸的酒精溶液,轻轻地向水面滴一滴溶液,油酸在水面上会很快散开,形成一油酸薄膜,待薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描出油酸薄膜的形状;
④将画有油酸薄膜轮廓形状的玻璃板,放在画有许多已知边长的小正方形的坐标纸上,计算出轮廓范围内正方形的总数,由小正方形边长和小正方形的总个数计算得此油膜面积为3.60×102cm2。
利用上述实验数据可求得油酸分子的直径为 m。(保留3位有效数字)
(3)(9分)如图所示,竖直放置的、左端封闭、右端开口的U形管中用水银柱封住一段空气柱L,当空气柱的温度为t1=7℃时,左臂水银柱的高度h1 =15cm,右臂水银柱的高度h2 =" 10" cm,气柱长度L1=20cm;仅将管内被封住的空气柱加热到t2=127℃且稳定时,图中的h1变为h1′= 10cm。不考虑水银和管的热胀冷缩,大气压强始终不变。当时的大气压强多大?(单位用cmHg)
在一个密闭的气缸内有一定质量的理想气体,如图所示是它从状态A 变化到状态B的V-T图象,己知AB的反向延长线通过坐标原点O,气体在A点的压.强为p=1.0x105 Pa,在从状态A变化到状态B的过程中,气体吸收的热量Q=7.0x102 J,求此过程中气体内能的增量△U
(1)以下说法正确的是 (选对一个给3分,选对两个给4分,选对3个给6分。每选错一个扣3分,最低得分为0分)
A.浸润现象是表面张力作用的结果,不浸润现象不是表面张力作用的结果
B.温度越高物体分子的平均动能越大
C.热量可以自发地由低温物体传到高温物体
D.压缩气体,气体的内能不一定增加
E.气体的体积变小,其压强可能减小
(2)如图所示,在一竖直放置的圆环形管道内封闭有一定质量的理想气体。用一绝热的固定活塞C和绝热、不计质量、可自由移动的活塞A将管道内气体分隔成体积相等的两部分,A、C与圆环的圆心O等高,两部分气体的温度均为T0 =300K。现保持下部分气体的温度不变,对上部分气体缓慢加热至T=500K,求此时活塞A的位置与O点的连线跟竖直方向OB之间的夹角θ。(不计两活塞的体积)