如图所示，粗细均匀的玻璃细管上端封闭，下端开口，竖直插在大而深的水银槽中，管内封闭有一定质量的空气，玻璃细管足够长，管内气柱长4 cm，管内外水银面高度差为10 cm。现将玻璃管沿竖直方向缓慢移动. （大气压强相当于75cmHg）求：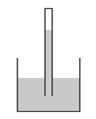
①若要使管内外水银面恰好相平，此时管内气柱的长度；
②若要使管内外水银面高度差为15 cm，玻璃管又应如何移动多少距离。
如图，一个粒子电荷量为q=8×10-3C，质量为m＝4×10－6kg，以速度v=2×103m/s穿过磁感强度B＝0.5T、宽度L＝1m的匀强磁场，粒子的重力不计，求：
（1）粒子穿出磁场时，速度方向与初速度方向之间的夹角为多少？
（2）当磁感强度B满足什么条件时，粒子将不能从右侧穿出磁场区域？
如图所示，水平放置的两平行金属板，板长为10 cm，两板相距2 cm.一束电子经加速电场后以v0＝4.0×107 m/s的初速度从两板中央水平射入板间，然后从板间飞出射到距板右端L为45 cm、宽D为20 cm的荧光屏上．(不计电子重力，荧光屏中点在两板间的中线上，电子质量m＝9.0×10－31 kg，电荷量e＝1.6×10－19 C)求：
(1)电子飞入两板前所经历的加速电场的电压；
(2)若偏转电压为720V，则电子射出偏转电场时的竖直方向的位移为多少？
(3)为使带电粒子能射中荧光屏所有位置，两板间所加电压的取值范围．
电路图2913甲所示，若电阻未知，电源电动势和内阻也未知，电源的路端电压U随电流I的变化图线及外电阻的U-I图线分别如图乙所示，求：
(1)电源的电动势和内阻；
(2)电源的路端电压；
(3)电源的输出功率．
如图所示，在匀强电场中，将带电荷量q＝－6×10－6 C的电荷从电场中的A点移到B点，克服电场力做了2.4×10－5 J的功，再从B点移到C点，电场力做了1.2×10－5 J的功．求：
(1)A、B两点间的电势差UAB和B、C两点间的电势差UBC；
(2)如果规定B点的电势为零，则A点和C点的电势分别为多少？
(3)作出过B点的一条电场线(只保留作图的痕迹，不写做法)．
粤公网安备 44130202000953号