高中物理动能定理试题

如图，从离子源产生的甲、乙两种离子，由静止经加速电压U加速后在纸面内水平向右运动，自M点垂直于磁场边界射入匀强磁场，磁场方向垂直于纸面向里，磁场左边界竖直。已知甲种离子射入磁场的速度大小为v ₁， 并在磁场边界的N点射出；乙种离子在MN的中点射出；MN长为l。不计重力影响和离子间的相互作用。求：

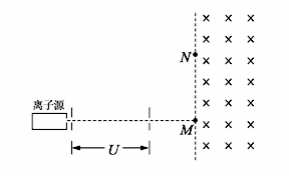
（1）磁场的磁感应强度大小；    

（2）甲、乙两种离子的比荷之比。    

如图，某同学用绳子拉动木箱，使它从静止开始沿粗糙水平路面运动至具有某一速度，木箱获得的动能一定（ ）

A．	小于拉力所做的功	B．	等于拉力所做的功
C．	等于克服摩擦力所做的功	D．	大于克服摩擦力所做的功

从地面竖直向上抛出一物体，物体在运动过程中除受到重力外，还受到一大小不变、方向始终与运动方向相反的外力作用。距地面高度 $\mathrm{h}$ 在 $3m$ 以内时，物体上升、下落过程中动能 ${\mathrm{E}}_k$ 随 $\mathrm{h}$ 的变化如图所示。重力加速度取 $10m/{\mathrm{s}}^2$ 。该物体的质量为（ ）

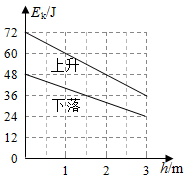
A．

$\mathrm{ }2\mathrm{kg}$

B．

$1.5\mathrm{kg}$

C．

$\mathrm{ }1\mathrm{kg }$

D．

$0.5\mathrm{kg}$

如图，在竖直平面内，一半径为R的光滑圆弧轨道ABC和水平轨道PA在A点相切。BC为圆弧轨道的直径。O为圆心，OA和OB之间的夹角为α，sinα= $\frac{3}{5}$ ，一质量为m的小球沿水平轨道向右运动，经A点沿圆弧轨道通过C点，落至水平轨道；在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用，已知小球在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零。重力加速度大小为g。求：

（1）水平恒力的大小和小球到达 C点时速度的大小；    

（2）小球到达 A点时动量的大小；    

（3）小球从 C点落至水平轨道所用的时间。    

如图，abc是垂直面内的光滑固定轨道，ab水平，长度为2R：bc是半径为R的四分之一的圆弧，与ac相切于b点。一质量为m的小球。始终受到与重力大小相等的水平外力的作用，自a点从静止开始向右运动，重力加速度大小为g。小球从a点开始运动到其他轨迹最高点，机械能的增量为（ ）

A．

$2\mathrm{mgR }$

B．

$4\mathrm{mgR }$

C．

$5\mathrm{mgR }$

D．

$\mathrm{ }6\mathrm{mgR}$

空间存在一方向竖直向下的匀强电场，O、P是电场中的两点。从O点沿水平方向以不同速度先后发射两个质量均为m的小球A、B。A不带电，B的电荷量为 $\mathrm{q}\mathrm{（}\mathrm{q}>0\mathrm{）}$ 。A从O点发射时的速度大小为 ${\mathrm{v}}_0$ ， 到达P点所用时间为 $\mathrm{t}$ ；B从O点到达P点所用时间为 $\frac{t}{2}$ 。重力加速度为 $\mathrm{g}$ ，求   

（1）电场强度的大小；    

（2）B运动到P点时的动能。    

如图，一平行板电容器连接在直流电源上，电容器的极板水平，两微粒a、b所带电荷量大小相等、符号相反，使它们分别静止于电容器的上、下极板附近，与极板距离相等。现同时释放a、b ， 它们由静止开始运动，在随后的某时刻t ， a、b经过电容器两极板间下半区域的同一水平面，a、b间的相互作用和重力可忽略。下列说法正确的是（ ）

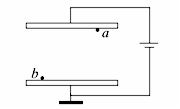
A. a的质量比 b的大 B. 在 t时刻， a的动能比 b的大

C. 在 t时刻， a和 b的电势能相等 D. 在 t时刻， a和 b的动量大小相等

为提高冰球运动员的加速能力，教练员在冰面上与起跑线距离 $s_0$ 和 $s_1$ $（s_1<s_0）$ 处分别设置一个挡板和一面小旗，如图所示。训练时，让运动员和冰球都位于起跑线上，教练员将冰球以初速度 $v_0$ 击出，使冰球在冰面上沿垂直于起跑线的方向滑向挡板；冰球被击出的同时，运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时，运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动，冰球到达挡板时的速度为 $v_1$ 。重力加速度大小为 $g$ 。求

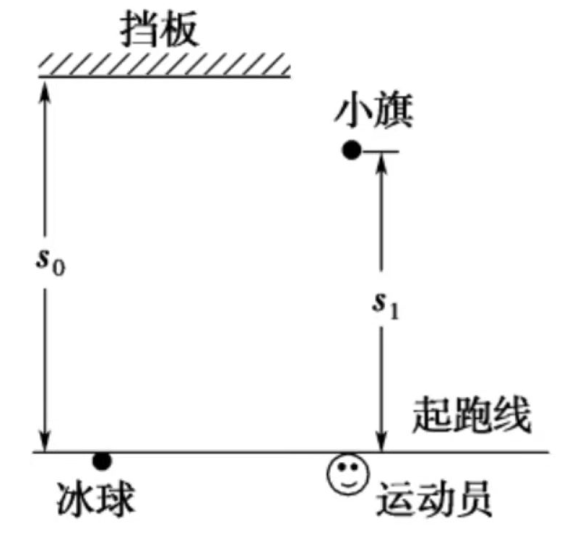
（1）冰球与冰面之间的动摩擦因数；

（2）满足训练要求的运动员的最小加速度。

一质量为m的烟花弹获得动能E后,从地面竖直升空,当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为E,且均沿竖直方向运动。爆炸时间极短,重力加速度大小为g,不计空气阻力和火药的质量,求    

（1）烟花弹从地面开始上升到弹中火药爆炸所经过的时间.   

（2）爆炸后烟花弹向上运动的部分距地面的最大高度.

一质量为m=2000 kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中，司机忽然发现前方100 m处有一警示牌。立即刹车。刹车过程中，汽车所受阻力大小随时间变化可简化为图（a）中的图线。图（a）中，0~t ₁时间段为从司机发现警示牌到采取措施的反应时间（这段时间内汽车所受阻力已忽略，汽车仍保持匀速行驶），t ₁=0.8 s；t ₁~t ₂时间段为刹车系统的启动时间，t ₂=1.3 s；从t ₂时刻开始汽车的刹车系统稳定工作，直至汽车停止，已知从t ₂时刻开始，汽车第1 s内的位移为24 m，第4 s内的位移为1 m。

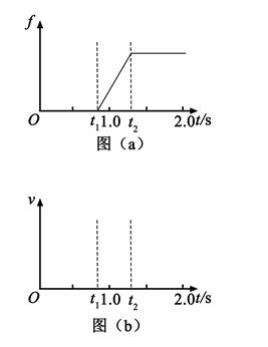
（1）在图（b）中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的 v- t图线；    

（2）求 t ₂时刻汽车的速度大小及此后的加速度大小；    

（3）求刹车前汽车匀速行驶时的速度大小及 t ₁~ t ₂时间内汽车克服阻力做的功；司机发现警示牌到汽车停止，汽车行驶的距离约为多少（以 t ₁~ t ₂时间段始末速度的算术平均值替代这段时间内汽车的平均速度）？

如图，两水平面（虚线）之间的距离为 $H$ ，其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为 $m$ 、电荷量分别为 $q$ 和 $–q（q>0）$ 的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域，并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下；M在电场中做直线运动，刚离开电场时的动能为 $N$ 刚离开电场时动能的1.5倍。不计空气阻力，重力加速度大小为 g。求

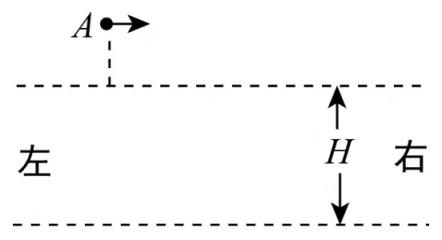
（1）M与N在电场中沿水平方向的位移之比；

（2）A点距电场上边界的高度；

（3）该电场的电场强度大小。

高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动，在启动阶段列车的动能（ ）          

A．

与它所经历的时间成正比

B．

与它的位移成正比

C．

与它的速度成正比

D．

与它的动量成正比

静止在水平地面上的两小物块A、B，质量分别为m _A=l.0 kg，m _B=4.0 kg；两者之间有一被压缩的微型弹簧，A与其右侧的竖直墙壁距离l=1.0m，如图所示。某时刻，将压缩的微型弹簧释放，使A、B瞬间分离，两物块获得的动能之和为E _k=10.0 J。释放后，A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为u=0.20。重力加速度取g=10 m/s²。A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。

   

（1）求弹簧释放后瞬间A、B速度的大小；    

（2）物块A、B中的哪一个先停止？该物块刚停止时A与B之间的距离是多少？    

（3）A和B都停止后，A与B之间的距离是多少？    

如图，两金属板P、Q水平放置，间距为d。两金属板正中间有一水平放置的金属网G，PQG的尺寸相同。G接地，PQ的电势均为 $\phi$ （ $\phi$ >0）。质量为m，电荷量为q（q>0）的粒子自G的左端上方距离G为h的位置，以速度v0平行于纸面水平射入电场，重力忽略不计。

（1）求粒子第一次穿过G时的动能，以及她从射入电场至此时在水平方向上的位移大小；    

（2）若粒子恰好从G的下方距离G也为h的位置离开电场，则金属板的长度最短应为多少？    

一质量为 $8.00\times {10}^{4}4\mathit{kg}$的太空飞船从其飞行轨道返回地面．飞船在离地面高度 $1.60\times {10}^{5}m$处以7.5×10³ m/s的速度进入大气层，逐渐减慢至速度为 $100m/s$时下落到地面．取地面为重力势能零点，在飞船下落过程中，重力加速度可视为常量，大小取为 $9.8m/s^2$． （结果保留2位有效数字）

（1）分别求出该飞船着地前瞬间的机械能和它进入大气层时的机械能；

（2）求飞船从离地面高度 $600m$处至着地前瞬间的过程中克服阻力所做的功，已知飞船在该处的速度大小是其进入大气层时速度大小的 $2.0\%$．