1990年3月，紫金山天文台将1965年9月20日发现的第2752号小行星命名为吴健雄星，其直径为32 km，如该小行星的密度和地球相同，已知地球半径R=6400km，地球的第一宇宙速度为8 km/s．求：该小行星第一宇宙速度？
我国的月球探测计划“嫦娥工程”分为“绕、落、回”三步。“嫦娥三号”的任务是“落”。 2013年12月2日，“嫦娥三号”发射，经过中途轨道修正和近月制动之后，“嫦娥三号”探测器进入绕月的圆形轨道I。12月12日卫星成功变轨，进入远月点P、近月点Q的椭圆形轨道II。如图所示。 2013年12月14日，“嫦娥三号”探测器在Q点附近制动，由大功率发动机减速，以抛物线路径下降到距月面100米高处进行30s悬停避障，之后再缓慢竖直下降到距月面高度仅为数米处，为避免激起更多月尘，关闭发动机，做自由落体运动，落到月球表面。
已知引力常量为G，月球的质量为M，月球的半径为R，“嫦娥三号”在轨道I上运动时的质量为m， P、Q点距月球表面的高度分别为h1、h2。
（1）求“嫦娥三号”在圆形轨道I上运动的速度大小；
（2）已知“嫦娥三号”与月心的距离为r时，引力势能为
（取无穷远处引力势能为零），其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中，动能和引力势能相互转化，它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v，请根据能量守恒定律求它经过P点时的速度大小；
一卫星绕某一行星表面附近做匀速圆周运动，其线速度大小为v。假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体重力，物体静止时，弹簧测力计的示数为N，已知引力常量为G，求这颗行星的质量。
2013年12月14日嫦娥三号成功实现了月球表面软着陆．嫦娥三号着陆前，先在距月球表面高度为h的圆轨道上运行，经过变轨进入远月点高度为h、近月点高度忽略不计的椭圆轨道上运行，为下一步月面软着陆做准备．已知月球半径为R，月球质量为M．
（1）求嫦娥三号在距月球表面高度为h的圆轨道上运行的周期T1；
（2）在开普勒第三定律
=k中，常数k可由嫦娥三号在圆轨道上运行的规律推出．求嫦娥三号在椭圆轨道上运行的周期T2．
太阳系外行星大多不适宜人类居住，绕恒星“Glicsc581”运行的行星“Gl-581c” 却很值得我们期待。该行星的温度在0℃到40℃之间，质量是地球的6倍，直径是地球的1.5倍、公转周期为13个地球日。“Glicsc581”的质量是太阳质量的0.31倍。设该行星与地球均视为质量分布均匀的球体，绕其中心天体做匀速圆周运动，则求：
（1）．如果人到了该行星，其体重是地球上的体重的多少倍？
（2）．该行星与“Glicsc581”的距离是日地距离的多少倍？（结果不用整理到最简，可带小数和根号）
（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即 k是一个对所有行星都相同的常量．将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式．已知引力常量为G，太阳的质量为M太．
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立．经测定月地距离为3.84×108m，月球绕地球运动的周期为2.36×106s，试计算地球的质量M地．（G=6.67×10-11Nm2/kg2，结果保留一位有效数字）
A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h，已知地球半径为R，地球自转角速度ω0，地球表面的重力加速度为g，O为地球中心。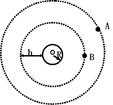
（1）求卫星B的运动周期
（2）如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近（O、B、A在同一直线上）则至少经过多长时间，它们再一次相距最近？
已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h．地球半径为R，地球表面的重力加速度为g，万有引力常量为G。求：
（1）地球的密度为多少？
（2）“天宫一号”在该圆轨道上运行时速度v的大小；
2013年12月14日嫦娥三号成功实现了月球表面软着陆．嫦娥三号着陆前，先在距月球表面高度为h的圆轨道上运行，经过变轨进入远月点高度为h、近月点高度忽略不计的椭圆轨道上运行，为下一步月面软着陆做准备．已知月球半径为R，月球质量为M．
（1）求嫦娥三号在距月球表面高度为h的圆轨道上运行的周期T1；
（2）在开普勒第三定律
=k中，常数k可由嫦娥三号在圆轨道上运行的规律推出．求嫦娥三号在椭圆轨道上运行的周期T2．
图为“嫦娥三号”探测器在月球上着陆最后阶段的示意图。首先在发动机作用下，探测器受到推力在距月面高度为h1处悬停（速度为0，h1远小于月球半径）；接着推力改变，探测器开始竖直下降，到达距月面高度为h2处的速度为υ；此后发动机关闭，探测器仅受重力下落到月面。已知探测器总质量为m（不包括燃料），地球和月球的半径比为k1，质量比为k2，地球表面附近的重力加速度为g。求：
（1）月球表面附近的重力加速度大小及探测器刚接触月面时的速度大小；
（2）从开始竖直下降到刚接触月面时，探测器机械能的变化。
天文观测到某行星有一颗以半径r、周期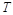
环绕该行星做匀速圆周运动的卫星，已知卫星质量为
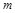，该行星的半径是卫星运动轨道半径的
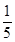．求：
（1）该行星的质量M；
（2）该行星表面处的重力加速度g．
继神秘的火星之后，土星也成了世界关注的焦点. 经过近7年时间，2亿千米在太空中风尘仆仆的穿行后，美航天局和欧航天局合作研究出“卡西尼”号土星探测器于美国东部时间6月30日（北京时间7月1日）抵达预定轨道，开始“拜访土星及其卫星家族. 这是人类首次针对土星及其31颗已知卫星最详尽的探测. 若“卡西尼”号土星探测器进入土星飞行的轨道，在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行，环绕n周飞行时间为t. （万有引力常量为G ）求：
（1） “卡西尼”号土星探测器绕土星运行的速度；
（2） 土星的质量；
（3） 土星上的第一宇宙速度；
一艘宇宙飞船绕一个不知名的、半径为R的行星表面飞行，环绕一周飞行时间为T（万有引力常量为G ），求：（1）该行星的平均密度ρ （2）该行星表面的重力加速度
已知地球同步卫星离地面的高度约为地球半径的6倍，若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，则该行星的的自转周期为多少小时？
粤公网安备 44130202000953号