月球绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天,(地球半径R地=6.4×103km,万有引力恒量为G。),(计算结果可以保留根号,且只要数量级对就给满分)
求:(1)地球同步卫星离地面的高度约为多少千米?
(2)地球的质量约为多少?
(3)月球绕地球运动的线速度 约为多少?
约为多少?
中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T=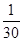 s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67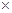 10
10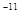 m
m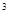 /kg.s
/kg.s )
)
由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同。已知地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为T,引力常量为G。假设地球可视为质量均匀分布的球体。求:
(1)质量为m的物体在地球北极所受地球对它的万有引力的大小;
(2)地球的半径;
(3)地球的密度。
已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h。地球半径为R,地球表面的重力加速度为g,万有引力常量为G。求:
(1)地球的密度为多少?
(2)“天宫一号”在该圆轨道上运行时速度v的大小;
双星系统中两个星球A、B的质量都是m,A、B相距L,它们正围绕两者连线上的某一点做匀速圆周运动。实际观测该系统的周期T要小于按照力学理论计算出的周期理论值 ,且
,且 ,于是有人猜测这可能是受到了一颗未发现的星球C的影响,并认为C位于双星A.B的连线正中间,相对A、B静止,求:
,于是有人猜测这可能是受到了一颗未发现的星球C的影响,并认为C位于双星A.B的连线正中间,相对A、B静止,求:
(1)两个星球A、B组成的双星系统周期理论值 ;
;
(2)星球C的质量。
双星系统由两颗彼此相距很近的两个恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的共同质量中心做周期相同的匀速圆周运动。现有一个天文观测活动小组为了测量一双星系统中的两个恒星的质量m1和m2,进行了如下测量:测出了该双星系统的周期T和质量为m1和m2的两个恒星的运动半径r1和r2。是根据上述测量数据计算出两个恒星的质量m1和m2。(万有引力恒量为G)
如图所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面内,离地面高度为h,已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心。求:
(1)卫星B的运行周期;
(2)若卫星B绕行方向与地球自转方向相同,某时刻A、B两 卫星相距最近(O、B、A在同一直线上),则至少经过多长时间,他们再一次相距最近?
已知一颗人造卫星在半径为R的某行星上空绕该行星做匀速圆周运动,经过时间t,卫星运动的弧长为s,卫星与行星的中心连线扫过的角度是θ弧度。(已知万有引力常量为G)求:
(1)人造卫星距该行量表面的高度h;
(2)该行量的质量M;
(3)该行量的第一宇宙速度v1。
我国的“探月工程”计划将在2017年宇航员登上月球.若宇航员登上月球后,以初速度v0竖直向上拋出一小球,测出小球从抛出到落回原处所需的 时间为t 。已知万有引力常量为G、月球的半径为 R ,不考虑月球自转的影响,求:
(1)求月球表面的重力加速度大小 ;
;
(2)月球的质量M ;
(3)飞船贴近月球表面绕月球做匀速圆周运动的周期T 。
如图为中国月球探测工程的想象标志,它以中国书法的笔触,勾勒出一轮明月和一双踏在其上的脚印,象征着月球探测的终极梦想。一位勤于思考的同学,为探月宇航员设计了如下实验:
在距月球表面高h处以初速度v0水平抛出一个物体,然后测量该平抛物体的水平位移为x。通过查阅资料知道月球的半径为R,引力常量为G,若物体只受月球引力的作用,请你求出:
(1)月球的密度 ;
;
(2)环绕月球表面的宇宙飞船的速率v。
某一行星有一质量为m的卫星,以半径r,周期T做匀速圆周运动,行星的半径是R,万有引力常量为G,求:
(1)行星的质量;
(2)行星表面的重力加速度是多少?
万有引力定律清楚的向人们揭示复杂运动的背后隐藏着简洁的科学规律,天上和地上的万物遵循同样的科学法则。
(1)当卡文迪许测量出引力常数G以后,他骄傲地说自己是“称量出地球质量”的人。当时已知地面的重力加速度g和地球半径R,根据以上条件,求地球的质量;
(2)随着我国“嫦娥三号”探测器降落月球,“玉兔”巡视器对月球进行探索,我国对月球的了解越来越深入。若已知月球半径为R月,月球表面的重力加速度为g月,嫦娥三号在降落月球前某阶段绕月球做匀速圆周运动的周期为T,试求嫦娥三号该阶段绕月球运动的轨道半径。
2009年2月天文学家发现了COROT-7b,其密度和地球接近,直径大约是地球的两倍。假定它的密度和地球的平均密度相等,直径等于地球直径的两倍,人们可以在该行星表面进行如下的物理活动。如图,货物传送带与水平地面间的夹角为θ,且有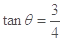 ,下端A与上端B之间的长度L=20m,传送带以v=8m/s的速度顺时针转动。将质量m=4kg的小物体轻放在传送带下端A处,物块与传送带之间的动摩擦因数μ=5/4。取地球表面重力加速度g= l0m/s
,下端A与上端B之间的长度L=20m,传送带以v=8m/s的速度顺时针转动。将质量m=4kg的小物体轻放在传送带下端A处,物块与传送带之间的动摩擦因数μ=5/4。取地球表面重力加速度g= l0m/s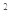 ,sinθ=0.6,cosθ=0.8,求:物块从A到B的过程中,传送带对物块做的功。
,sinθ=0.6,cosθ=0.8,求:物块从A到B的过程中,传送带对物块做的功。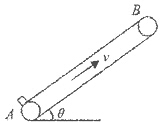
假设一卫星在距地面R高处做匀速圆周运动,已知地球的半径为R,地面的重力加速度为g。试求:
(1)卫星运行的线速度大小;(2)卫星运行的周期。