高中物理万有引力定律及其应用计算题

物体在距某一行星表面某一高度的O点由静止开始做自由落体运动，依次通过A、B、C三点，已知AB段与BC段的距离相等，均为24 cm，通过AB与BC的时间分别为0.2 s与0.1 s，若该星球的半径为180 km，则环绕该行星的卫星做圆周运动的最小周期为多少？

“嫦娥一号”和“嫦娥二号”卫星相继完成了对月球的环月飞行，标志着我国探月工程的第一阶段已经完成。设“嫦娥二号”卫星环绕月球的运动为匀速圆周运动，它距月球表面的高度为h，已知月球的半径为R，月球表面重力加速度为g,求“嫦娥二号”卫星绕月球运动的周期。

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。

宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其他星体对它们的引力作用．现已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆轨道运行．设每个星体的质量均为m，引力常量为G.
(1)试求第一种形式下，星体运动的线速度大小和周期；
(2)假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？

如图1所示，在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动，小球在最低点与最高点所受轻绳的拉力之差为ΔF，假设星球是均匀球体，其半径为R，已知万有引力常量为G，不计一切阻力。

（1）求星球表面重力加速度
（2）求该星球的密度
（3）如图所示2，在该星球表面上，某小球以大小为v₀的初速度平抛，恰好能击中倾角为θ的斜面，且位移最短，试求该小球平抛的时间

我国探月工程已规划至“嫦娥四号”，并计划在2017年将嫦娥四号探月卫星发射升空。到时将实现在月球上自动巡视机器人勘测。已知万有引力常量为G，月球表面的重力加速度为g，月球的平均密度为ρ，月球可视为球体，球体积计算公式。求：
（1）月球质量M；
（2）嫦娥四号探月卫星在近月球表面做匀速圆周运动的环绕速度v。

2013年12月14日晚，嫦娥三号探测器成功落月，这是中国首次实现地外天体软着陆，着陆器落月过程的最后时刻，有以上几个关键阶段：①着陆器距离月面100m时保持悬停，对着陆区进行检测，选择安全的着陆点；②随后发动机维持一定推力缓慢下降，降至距月面4m时关闭发动机，着陆器依靠自身重力在月面着陆．已知月球半径约为地球半径的，月球质量约为地球质量的，着陆器质量约为1000kg，地球表面重力加速度g=10m/s²，根据以上数据计算：
（1）着陆器距月面100m悬停时，发动机产生的推力为多大？
（2）若关闭发动机时速度为零，则最后依靠自身重力着陆，落至月面的速度为多大？

2012年6月16日，“神舟九号”宇宙飞船搭载3名航天员飞天，并于6月18日14∶00与“天宫一号”成功对接。在发射时，“神舟九号”宇宙飞船首先要发射到离地面很近的圆轨道，然后经过多次变轨后，最终与在距地面高度为h的圆形轨道上绕地球飞行的“天宫一号”完成对接，之后，整体保持在距地面高度仍为h的圆形轨道上绕地球继续运行．已知地球半径为R，地面附近的重力加速度为g。求：
（1）地球的第一宇宙速度；
（2）“神舟九号”宇宙飞船在近地圆轨道运行的速度与对接后整体的运行速度之比。

用天文望远镜长期观测，人们在宇宙中发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质存在的形式和分布有了较深刻的认识，双星系统是由两个星体构成，其中每个星体的线度都小于两星体间的距离，一般双星系统距离其它星体很远，可以当做孤立系统处理，现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。万有引力常量为G。
（1）计算该双星系统的运动周期T_计算。
（2）若实验上观测到的运动周期为T_观测，且T_观测：T_计算=1： (N>1)，为了解释T_观测与T_计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质，作为一种简化模型，我们假定在这两个星体连线为直径的球体内均匀分布着暗物质，而不考虑其它暗物质的影响，试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。

如图所示一宇航员站在一星球表面，用一根细绳一端固定在O点，另一端固定质量为m的小球，在最低点给小球某一速度让小球在竖直平面内做完整圆周运动，小球运动到最低点和最高点绳的拉力差为F，已知该星球的半径为R，万有引力常量为G。求该星球的质量M。

2012年6月18日神舟九号飞船与天宫一号目标飞行器在离地343km的近圆轨道上成功进行了我国首次载人空间交会对接。若神舟九号飞船绕地球运动视为在赤道平面内的匀速圆周运动，离地高度h=300km。已知地球半径R=6.4×10³km，地面重力加速度g=9.8m/s²。（结果保留2位有效数字，先写出表达式再求出数值）
求：①神舟九号飞船运动的周期T；
②若地球的自转周期为T₀=8.6×10⁴s，则神舟九号飞船连续两次经过赤道上某一建筑物的时间间隔Δt。

(10分)在天体运动中，把两颗相距较近的恒星称为双星，已知A、B两恒星质量分别为m₁和m₂，两恒星相距为L，两恒星分别绕共同的圆心做圆周运动，如图所示，求两恒星的轨道半径和角速度？（已知万有引力常量为G）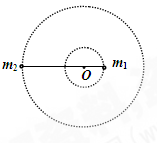

假设地球可视为质量均匀分布的球体。已知地球质量为M，半径为R，自转的周期为T，引力常量为G。求：
（1）地球同步卫星距离地面的高度H；
（2）地球表面在两极的重力加速度g；
（3）地球表面在赤道的重力加速度g₀。

已知引力常量G，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T₁，地球的自转周期T₂，地球表面的重力加速度g，某同学根据以上条件，提出一种估算地球质量M的方法：同步卫星绕地心做圆周运动，由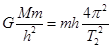得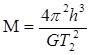
（1）请判断上面的结果是否正确，并说明理由，如不正确，请给出正确的解法和结果；
（2）请根据已知条件再提出两种估算地球质量的方法并解得结果（用上面所给的已知量表示）。

石墨烯是近些年发现的一种新材料，其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化，其发现者由此获得2010年诺贝尔物理学奖．用石墨烯制作超级缆绳，人类搭建“太空电梯”的梦想有望在本世纪实现．科学家们设想，通过地球同步轨道站向地面垂下一条缆绳至赤道基站，电梯仓沿着这条缆绳运行，实现外太空和地球之间便捷的物资交换．

(1) 有关地球同步轨道卫星，下列表述正确的是：
A.卫星距离地面的高度大于月球离地面的高度
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时可能经过嘉兴的正上方
D.卫星运行的向心加速度小于地球表面的重力加速度
(2) 若把地球视为质量分布均匀的球体，已知同步卫星绕地球做匀速圆周运动的向心加速度大小为a₁，近地卫星绕地球做匀速圆周运动的向心加速度大小为a₂,地球赤道上的物体做匀速圆周运动的向心加速度大小为a₃，地球北极地面附近的重力加速度为g₁，地球赤道地面附近的重力加速度为g₂，则：
A. a₁=g₁        B. a₂=g₁       C. a₃=g₁        D. g₁ -g₂=a₃
(3)当电梯仓停在距地面高度h＝4R的站点时，求仓内质量m＝50kg的人对水平地板的压力大小．取地面附近重力加速度g取10m/s²，地球自转角速度ω＝7.3×10^－5rad/s，地球半径R＝6.4×10³km.（结果保留三位有效数字）