高中物理万有引力定律及其应用计算题

宇航员站在一星球表面h高处，以初速度沿水平方向抛出一个小球，球落到星球表面的水平射程为S，已知该星球的半径为R，引力常量为G，求：该星球的质量M。

物体在地球表面重16 N，它在以5 m/s²的加速度加速上升的火箭中的视重为9 N，则此火箭离地球表面的距离为地球半径的多少倍？（设地球表面处g₀取10 m/s²）

“嫦娥一号”探月卫星在环绕月球的极地轨道上运动，由于月球的自转，因而“嫦娥一号”卫星能探测到整个月球表面。2007年12月11日“嫦娥一号”卫星的CCD相机已对月球背面进行成像探测，并获得了月球背面部分区域的影像图。卫星在绕月极地轨道上做圆周运动时距月球表面高为H，绕行的周期为T_M；月球绕地公转的周期为T_E，半径为R₀；地球半径为R_E，月球半径为R_M。试解答下列问题：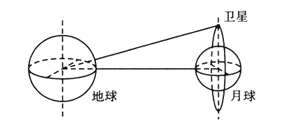

（1）若忽略地球及太阳引力对绕月卫星的影响，试求月球与地球的质量之比。
（2）若当绕月极地轨道的平面与月球绕地公转的轨道平面垂直，也与地心到月心的连线垂直（如图所示）时，探月卫星将向地球发送所拍摄的照片。已知光速为c，则此照片信号由探月卫星传送到地球最短需要多长时间？

“嫦娥一号” 的成功发射，为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道近似圆周，距月球表面的高度为H，飞行周期为T,月球的半径为R，万有引力常量为G，假设宇航员在飞船上,飞船在月球表面附近竖直平面内俯冲， 在最低点附近作半径为r的圆周运动，宇航员质量是m，飞船经过最低点时的速度是v；。求：(1)月球的质量M是多大？ (2)经过最低点时，座位对宇航员的作用力F是多大？

如图所示，在距离一质量为M、半径为R、密度均匀的球体R远处有一质量为m的质点。此时M对m的万有引力为F₁，当从M中挖去一半径为R/2的球体时，剩余部分对m的万有引力为F₂，则F₁与F₂的比值为多少？

已知引力常量G，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T₁，地球的自转周期T₂，地球表面的重力加速度g，某同学根据以上条件，提出一种估算地球质量M的方法：同步卫星绕地心做圆周运动，由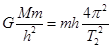得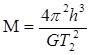
（1）请判断上面的结果是否正确，并说明理由，如不正确，请给出正确的解法和结果；
（2）请根据已知条件再提出两种估算地球质量的方法并解得结果（用上面所给的已知量表示）。

某天体的半径为地球半径的2倍，质量为地球质量的1/8倍，求该天体的第一宇宙速度及该天体表面处的重力加速度。（已知地球的第一宇宙速度为8km/s，地球表面的重力加速度为10m/s²。）结果保留2位有效数字

经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当做孤立系统来处理。现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。试求：
（1）该双星系统的运动周期；
（2）若该实验中观测到的运动周期为T_观测，且。为了理解T_观测 与T_计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度。

我国“神舟”五号飞船于2003年l0月15日在酒泉航天发射场由长征二号F运载火箭成功发射升空，若长征二号F运载火箭和飞船起飞时总质量为1.0×10⁵kg，起飞推动力为3.0×10⁶N，运载火箭发射塔高160m，试问：（g=10m/s²）
（1）运载火箭起飞时的加速度为多大？
（2）假如运载火箭起飞时推动力不变，忽略一切阻力和运载火箭质量的变化，试确定运载火箭需经多长时间才能飞离发射塔？
（3）这段时间内飞船中的宇航员承受了多大的压力？（设宇航员的质量为65kg）

在半径R＝5000 km 的某星球表面，宇航员做了如下实验．实验装置如图甲所示，竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m＝0.2 kg 的小球从轨道AB上高H处的某点静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．求：

（1）圆轨道的半径．
（2）该星球的第一宇宙速度．

如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们还能相距最近？

一个质量为1500 kg行星探测器从某行星表面竖直升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭；如图所示为探测器从发射到落回出发点全过程的速度图象；已知该行星表面没有大气，不考虑探测器总质量的变化；求：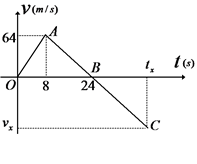

（1）探测器在行星表面上升达到的最大高度；
（2）探测器落回出发点时的速度；
（3）探测器发动机正常工作时的推力。

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。

“嫦娥三号”是我国嫦娥工程第二阶段的登月探测器，于2013年12月2日凌晨l时30分在西昌卫星发射中心发射，携“玉兔号”月球车奔向距地球38万千米的月球；6日17时53分，“嫦娥三号”成功实施近月制动，顺利进入距月面平均高度约100千米的环月轨道；14日21时11分在月球正面的虹湾地区，“嫦娥三号”又成功实现月面软着陆，开始对月表形貌与地质构造等进行科学探测。若“嫦娥三号”环月飞行时运行周期为T，环月轨道（图中圆轨道Ⅰ）距月球表面高为h。已知月球半径为R，引力常量为G，求：

（1）月球的质量；
（2）月球表面的重力加速度。

随着航天技术的不断发展，人类宇航员可以乘航天器登陆一些未知星球。一名宇航员在登陆某星球后为了测量此星球的质量进行了如下实验：他把一小钢球托举到距星球表面高度为h处由静止释放，计时仪器测得小钢球放到落回星球表面的时间为t。此前通过天文观测测得此星球的半径为R，已知万有引力常量为G，不计小钢球下落过程中的气体阻力，可认为此星球表面的物体受到的重力等于物体与星球之间的万有引力。求：
(1）此星球表面的重力加速度g；
(2）此星球的质量M；及第一宇宙速度
(3）若距此星球表面高H的圆形轨道有一颗卫星绕它做匀速圆周运动，求卫星的运行周期T。