高中物理万有引力定律及其应用试题

为了实现登月计划，先要测算地月之间的距离。已知地球表面重力加速度为g，地球半径为R，在地面附近物体受到地球的万有引力近似等于物体在地面上的重力，又知月球绕地球运动的周期为T，万有引力常量为G。则：
（1）地球的质量为多少？（2）地月之间的距离约为多少？

“黑洞”是爱因斯坦的广义相对论中预言的一种特殊天体，它的密度极大，对周围的物质（包括光子）有极强的吸引力，根据爱因斯坦理论，光子是有质量的，光子到达黑洞表面时也将被吸入，最多恰能绕黑洞表面做圆周运动，天文学家通过天文观测认为：在“猎户座”可能存在着一个“黑洞”，距“黑洞”中心km处有一颗恒星以200km／s的速度绕其旋转。根据以上信息，试估算这一“黑洞”的半径R=_____m。（已知c=3×10⁵km／s保留一位有效数字）

已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v₁的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。

年月,"嫦娥二号冶成功进入了环绕"日地拉格朗日点冶的轨道,我国成为世界上第三个造访该点的国家. 如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的（）

A．	线速度大于地球的线速度
B．	向心加速度大于地球的向心加速度
C．	向心力仅由太阳的引力提供
D．	向心力仅由地球的引力提供

两个物体之间的万有引力大小为F₁，若两物体之间的距离减少x，两物体仍视为质点。此时两者之间的万有引力为F₂，根据上述条件可以计算       (      )

A．两物体的质量	B．万有引力恒量
C．两物体之间的距离	D．条件不足，无法计算上三项

对于万有引力定律的表达式F=Gm₁m₂/r²，下列说法中正确的是（     ）

A．公式中G为引力常量，它是由实验测得的，不是人为规定的

B．当r趋于零时，万有引力趋于无穷大

C．m1与m2受到的引力总是大小相等的，与m1、m2是否相等无关

D．m1与m2受到的引力总是大小相等的、方向相反的，是一对平衡力

已知月球绕地球运动周期T和轨道半径r，地球半径为R求（1）地球的质量？（2）地球的平均密度？

为了验证地面上物体的重力与地球吸引月球、太阳吸引行星的力是否为同一性质的力，遵循同样的规律，牛顿曾经做过著名的月—地检验，其基本想法是：如果重力和星体间的引力是同一性质的力，都与距离的            关系，因为月心到地心的距离是地球半径的60倍，那么月球绕地球做近似圆周运动的向心加速度就应该是地面重力加速度的       倍，牛顿通过计算证明他的想法是正确的。

已知太阳到地球与地球到月球的距离的比值约为390，月球绕地球旋转的周期约为27天．利用上述数据以及日常的天文知识，可估算出太阳对月球与地球对月球的万有引力的比值约为 (    )

A．0.2

B．2

C．20

D．200

土星周围有美丽壮观的“光环”，组成环的颗粒是大小不等、线度从1μm到10m的岩石、尘埃，类似于卫星，它们与土星中心的距离从7.3×10⁴km延伸到1.4×10⁵km。已知环的外缘颗粒绕土星做圆周运动的周期约为14h，引力常量为6.67×10^-11NŸm²/kg²，则土星的质量约为（估算时不考虑环中颗粒间的相互作用） （   ）

A．9.0×10^16kg

B．6.4×10^17kg

C．9.0×10^25kg

D．6.4×10^26kg

某中子星的质量大约与太阳的质量相等，为2×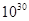kg，但是它的半径才不过10km，求：（1）此中子星表面的自由落体加速度。
（2）贴近中子星表面，沿圆轨道运动的小卫星的速度。
（已知引力常量为G=6.67×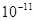N   ）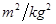

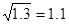
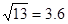地球的半径为R，地面的重力加速度为g，一颗离地面高度为R的人造地球卫星绕地球做匀速圆周运动，则（　   　）

A．卫星加速度的大小为	B．卫星运转的角速度为
C．卫星运转的线速度为	D．卫星运转的周期为

火星的质量和半径分别为地球的1/10和1/2，地球表面的重力加速度为g，则火星表面的重力加速度为（     ）

A．0.2g

B．0.4g

C．2.5g

D．5g

(12分)我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成，这极大的提高了同学们对月球的关注程度。以下是某同学就有关月球的知识设计的两个问题，请你解答：
⑴若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
⑵若某位宇航员随登月飞船登陆月球后，在月球表面某处以速度v₀竖直向上抛出一个小球，经过时间t，小球落回到抛出点。已知月球半径为R_月，万有引力常量为G。试求出月球的质量M_月。

已知引力常量为G，地球的质量为M，地球自转的角速度为ω₀，月球绕地球转动的角速度为ω，假设地球上有一棵苹果树长到了接近月球那么高，则此树顶上一只苹果的线速度大小为___________，此速度___________（选填“大于”、“等于”或“小于”）月球绕地球运转的线速度。