高中物理万有引力定律及其应用试题

如图所示，两球的半径远小于，而球质量分布均匀，大小分别为、，则两球间的万有引力的大小为（  ）

A．	B．
C．	D．

下列说法正确的是（ ）

A．第一宇宙速度是人造卫星环绕地球运动的速度

B．第一宇宙速度是人造卫星在地面附近绕地球做匀速圆周运动所必须具有的速度

C．如果需要，地球同步通讯卫星可以定点在地球上空的任何一点

D．地球同步通讯卫星的轨道可以是圆的也可以是椭圆的

万有引力定律首次揭示了自然界中物体间一种基本相互作用的规律.以下说法正确的是

A．物体的重力不是地球对物体的万有引力引起的

B．人造地球卫星离地球越远，受到地球的万有引力越大

C．人造地球卫星绕地球运动的向心力由地球对它的万有引力提供

D．宇宙飞船内的宇航员处于失重状态是由于没有受到万有引力的作用

已知引力常量G和下面的哪组数据，不能算出地球的质量M_地（   ）

A．月球绕地球运动的周期T１及月球到地球中心的距离R1

B．地球绕太阳运行周期T2及地球到太阳中心的距离R2

C．人造卫星在地面附近的运行速度v3和运行周期T3

D．地球表面的重力加速度g及地球半径R

日本物理学家小林诚和益川敏英由于发现了对称性破缺的起源，并由此预言的六个夸克逐渐被实验证实，获得2008年诺贝尔物理学奖．夸克之间的强相互作用势能可写为，式中r是正、反顶夸克之间的距离，a_s＝0．12是强相互作用耦合系数，k₂是与单位制有关的常数，在国际单位制中k₂=0．319×10^-25J·m；而在电荷之间的相互作用中，相距为r，电荷量分别为q₁q₂的两个点电荷之间的电势能，式中k₁是静电力常量．根据题中所给信息可以判定下列说法正确的是 （    ）

A．正反顶夸克之间的相互作用力为

B．正反顶夸克之间的相互作用力为

C．若地球质量为M，则轨道半径为r，质量为m的地球卫星的万有引力势能为

D．若地球质量为M，则轨道半径为r、质量为m的地球卫星的万有引力势能为

我国自主研制的“北斗一号”卫星导航系统，在甘肃玉树的抗震救灾中发挥了巨大作用．北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能．“北斗”系统中两颗工作星均绕地心O做匀速圆周运动，轨道半径为r，某时刻两颗工作卫星分别位于轨道上的A、B两位置（如图所示）．若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中正确的是 （   ）

A．卫星1向后喷气加速，一定能追上卫星2
B．这两颗卫星的加速度大小相等，均为
C．卫星1由位置A运动到位置B所需的时间为
D．卫星1由位置A运动到位置B的过程中万有引力做正功

下面关于万有引力的说法中正确的是                                    

A．重力和万有引力是两种不同性质的力

B．万有引力是普遍存在于宇宙中所有具有质量的物体之间的相互作用

C．当两物体间有另一质量不可忽略的物体存在时，则这两个物体间的万有引力将增大

D．当两物体间距为零时，万有引力将无穷大

有关万有引力的说法中，正确的有：

A．物体落到地面上，说明地球对物体有引力，物体对地球没有引力

B．中的G是比例常数，适用于任何两个物体之间，它没有单位

C．万有引力定律是牛顿在总结前人研究的基础上发现的

D．地面上自由下落的苹果和天空中运行的月亮，受到的都是地球引力

对于万有引力定律的表达式，下列说法中正确的是（  ）

A．公式中为引力常量，它的大小是牛顿通过扭秤实验测定的

B．当趋于零时，任意两个物体间的万有引力都趋于无限大

C．若，则受到的引力大

D．该公式不适用强引力的计算

我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成，这极大地提高了同学们对月球的关注程度．以下是某同学就有关月球的知识设计的问题，请你解答：若已知地球半径为，地球表面的重力加速度为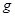，月球绕地球运动的周期为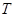，且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。

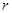一物体在某行星表面受的万有引力是它在地球表面受到的万有引力的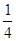。在地球走得很准的摆钟搬到此行星上后，此钟的分针走一整圈所经历的时间实际上是（   ）

A．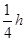

B．

C．2h

D．4h

宇航员在地球表面从某一高度自由落下一小球，经过时间t小球落回地面；若他在某星球表面从相同的高度自由落下同一小球，需经过时间2t小球落回表面．(取地球表面重力加速度g＝10 m/s²，空气阻力不计)。则该星球表面附近的重力加速度g′=___________；已知该星球的半径与地球半径之比为R_星∶R_地＝1∶4，求该星球的质量与地球的质量之比M_星∶M_地．=____________________

假如一做圆周运动的人造地球卫星的轨道半径增加到原来的2倍，仍做圆周运动，则

A．根据公式v＝ωr可知卫星运动的线速度将增大到原来的2倍

B．根据公式F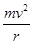＝可知卫星所需的向心力将减小到原来的1/2

C．根据公式F＝G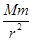可知地球提供的向心力将减小到原来的1/4

D．根据上述B和C中给出的公式可知，卫星运行的线速度将减小到原来的1/2

两颗人造卫星A、B的质量之比m_A∶m_B=1∶2，轨道半径之比r_A∶r_B=1∶3，某一时刻它们的连线通过地心，则此时它们的线速度之比v_A∶v_B=        ，向心加速度之比a_A∶a_B=      ，向心力之比F_A∶F_B=          。

地核的体积约为整个地球体积的16%，地核的质量约为地球质量的34%.经估算，地核的平均密度为_______kg/m³.（已知地球半径为6.4×10⁶ m，地球表面重力加速度为9.8 m/s²，万有引力常量为6.7×10^－11N·m²/kg²，结果取两位有效数字。）