高中物理平抛运动计算题

如图所示，半径R=0.9m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点B与长为L=1m的水平面相切于B点，BC离地面高h=0.45m，C点与一倾角为的光滑斜面连接，质量m=1.0kg的小滑块从圆弧顶点D由静止释放，已知滑块与水平面间的动摩擦因数，取g=10m／s²．

求：（1）小滑块刚到达圆弧的B点时对圆弧的压力：
（2）小滑块到达C点时速度的大小：
（3）小滑块从C点运动到地面所需的时间．

(18分)在“极限”运动会中，有一个在钢索桥上的比赛项目．如图所示，总长为的均匀粗钢丝绳固定在等高的、处，钢丝绳最低点与固定点、的高度差为，动滑轮起点在处，并可沿钢丝绳滑动，钢丝绳最低点距离水面也为．若质量为的人抓住滑轮下方的挂钩由点静止滑下，最远能到达右侧点，、间钢丝绳相距为，高度差为 ．若参赛者在运动过程中始终处于竖直状态，抓住滑轮的手与脚底之间的距离也为，滑轮与钢丝绳间的摩擦力大小视为不变，且摩擦力所做功与滑过的路程成正比，不计参赛者在运动中受到的空气阻力、滑轮（含挂钩）的质量和大小，不考虑钢索桥的摆动及形变．

（1）滑轮与钢丝绳间的摩擦力是多大？
（2）若参赛者不依靠外界帮助要到达点，则人在点处抓住挂钩时至少应该具有多大的初动能？
（3）比赛规定参赛者须在钢丝绳最低点脱钩并到达与钢丝绳最低点水平相距为、宽度为，厚度不计的海绵垫子上．若参赛者由点静止滑下，会落在海绵垫子左侧的水中．为了能落到海绵垫子上，参赛者在点抓住挂钩时应具有初动能的范围？

(18分)如图，质量m=20kg的物块（可视为质点），以初速度v₀=10m/s滑上静止在光滑轨道的质量M=30kg、高h=0.8m的小车的左端，当车向右运动了距离d时（即A处）双方达到共速。现在Ａ处固定一高h=0.8m、宽度不计的障碍物，当车撞到障碍物时被粘住不动，而货物继续在车上滑动，到A处时即做平抛运动，恰好与倾角为53°的光滑斜面相切而沿斜面向下滑动，已知货物与车间的动摩擦因数μ=0.5。
（g=10m/s²，sin53°=0.8，cos53°=0.6）求：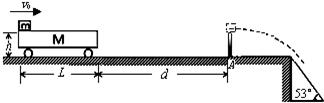

(1)车与货物共同速度的大小v₁；
(2)货物平抛时的水平速度v₂；
(3)车的长度Ｌ与距离d．

我人民海军进行某次登陆演练，假设一艘战舰因吨位大，吃水太深，只能停锚在离海岸某处。登陆队员需要从较高的军舰甲板上，利用绳索下滑到登陆快艇上再行登陆接近目标，若绳索两端固定好后，与竖直方向的夹角θ=30°，队员甲先匀加速滑到某最大速度，再靠摩擦匀减速滑至快艇，速度刚好为零，在队员甲开始下滑时，队员乙在甲板上同时从同一地点开始向快艇以速度v₀=m／s平抛救生圈，第一个刚落到快艇上时，紧接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇上的同一位置，取g=10m／s²，不计空气阻力，求：

（1）军舰甲板到快艇的竖直高度H；
（2）队员甲在绳索上运动的时间t₀及队员甲在下滑过程中的最大速度v₁；
（3）若登陆快艇一开始停在离海岸S=1km处（如图），登陆快艇额定功率P=5kw，载人后连同装备总质量m=10³kg，从静止开始以额定功率向登陆点加速靠近，到达岸边时刚好能达到最大速度v₂=10m／s，求登陆艇运动的时间t'。

如图所示，用内壁光滑的薄壁细圆管弯成的由半圆形APB（圆半径比细管的内径大得多）和直线BC组成的轨道固定在水平桌面上，已知APB部分的半径R＝1.0 m，BC段长L＝1.5m。弹射装置将一个小球(可视为质点)以v₀＝5m/s的水平初速度从A点弹入轨道，小球从C点离开轨道随即水平抛出，落地点D离开C的水平距离s＝2m，不计空气阻力，g取10m/s²。求：

（1）小球在半圆轨道上运动时的角速度ω和加速度a的大小；
（2）小球从A点运动到C点的时间t；
（3）桌子的高度h。

如图所示，光滑曲面AB与水平地面BC相切于B，竖直光滑半圆轨道CD与水平地面BC切于C，已知圆轨道半径为R，BC长为4R，且表面粗糙，一滑块从AB轨道上距地面4R高度处由静止释放，之后能够通过圆轨道的最高点D，且对D处的压力为0，求：

（1）若从曲面上距地2R高度处无初速释放滑块，滑块将停在何处；
（2）若使滑块通过D处后水平抛出，刚好击中地面上的B点，应从AB轨道上离地面多高处由静止释放滑块．

如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的1/4圆周轨道，半径OA处于水平位置，BDO是直径为15m的半圆轨道，D为BDO轨道的中央。一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的倍。取g=10m/s²。

（1）H的大小？
（2）试讨论此球能否到达BDO轨道的O点，并说明理由。
（3）小球沿轨道运动后再次落到轨道上的速度的大小是多少？

一只质量为2kg的小球，从距水平地面5m高的点以10m/s的初速度水平抛出．不计空气阻力，取重力加速度g=10m/s²．求：

（1）小球刚抛出时相对于水平地面的重力势能；
（2）小球在空中飞行的时间；
（3）小球抛出的水平距离．

(15分)如图甲所示，弯曲部分AB和CD是两个半径相等的1/4圆弧，中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)，分别与上下圆弧轨道相切连接，BC段的长度L可作伸缩调节，下圆弧轨道与地面相切，其中D、A分别是上、下圆弧轨道的最高点与最低点，整个轨道固定在竖直平面内，一小球多次以某一速度从A点水平进入轨道而从D点水平飞出，今在A、D两点各放一个压力传感器，测试小球对轨道A、D两点的压力，计算出压力差ΔF，改变BC的长度L，重复上述实验，最后绘得的ΔF-L图象如图乙所示。(不计一切摩擦阻力，g取10m/s²)

⑴某一次调节后，D点的离地高度为0.8m，小球从D点飞出，落地点与D点的水平距离为2.4m，求小球经过D点时的速度大小；
⑵求小球的质量和弯曲圆弧轨道的半径。

一位同学玩飞镖游戏，已知飞镖距圆盘为L，且对准圆盘上边缘的A点水平抛出，初速度为v₀ ，飞镖抛出的同时，圆盘以垂直盘面且过盘心O点的水平轴匀速转动。若飞镖恰好击中A点，空气阻力忽略不计，重力加速度为g，求：

（1）飞镖打中A点所需的时间；
（2）圆盘的半径r；
（3）圆盘转动角速度的可能值。

如图所示的“S”形玩具轨道，该轨道是用内壁光滑的薄壁细圆管弯成，放置在竖直平面内，轨道弯曲部分是由两个半径相等的半圆对接而成，圆半径比细管内径大得多，轨道底端与水平地面相切，轨道在水平面上不可移动。弹射装置将一个小球（可视为质点）从a点水平弹射向b点并进入轨道，经过轨道后从最高点d水平抛出。已知小球与地面ab段间的动摩擦因数μ=0.2，不计其它机械能损失，ab段长L=1.25m，圆的半径R=0.1m，小球质量m=0.01kg，轨道质量为M=0.26kg，g=10m/s²，求：

（1）要使小球从d点抛出后不碰轨道，小球的初速度v₀需满足什么条件？
（2）设小球进入轨道之前，轨道对地面的压力大小等于轨道自身的重力，当v₀至少为多少时，小球经过两半圆的对接处c点时，轨道对地面的压力为零。
 

如图所示，半径为R=0.2m的光滑1/4圆弧AB在竖直平面内，圆弧B处的切线水平。B端高出水平地面h=0.8m，O点在B点的正下方。将一质量为m=1.0kg的滑块从A点由静止释放，落在水平面上的C点处，（g取10m/s²）求：

（1）滑块滑至B点时对圆弧的压力及落地点C到O的距离；
（2）在B端接一长为L=1.0m的木板MN，滑块从A端释放后正好运动到N端停止，求木板与滑块的动摩擦因数μ；
（3）若将木板右端截去长为ΔL的一段，滑块从A端释放后将滑离木板落在水平面上P点处，要使落地点P距O点的最远，ΔL应为多少？

如图所示，质量 m＝2 kg 的小球以初速度 v₀沿光滑的水平面飞出后，恰好无碰撞地进入光滑的圆弧轨道，其中圆弧 AB 对应的圆心角θ＝53°，圆半径 R＝0.5 m．若小球离开桌面运动到 A 点所用时间t＝0.4 s . (sin53°＝0.8,cos53°＝0.6，g＝10 m/s²)

（1）求小球沿水平面飞出的初速度 v₀的大小？
（2）到达 B 点时，求小球此时对圆弧的压力大小？
（3）小球是否能从最高点 C 飞出圆弧轨道，并说明原因.

(19分)如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量、电量的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度，倾斜轨道与水平方向夹角为、倾斜轨道长为，带电小球与倾斜轨道的动摩擦因数。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强。（cos37°=0.8，sin37°=0.6，取g=10m/s²）求：

（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？

如图所示，倾角为θ的粗糙斜面的底端有一凹形小滑块，在底端竖直线上离底端高度为H处有一个小球，小球以一定的水平速度v₀抛出。

（1）要使小球垂直打在斜面上，试推导小球离斜面底端的高度H与小球速度v₀之间的关系。
（2）若斜面倾角θ=37°，凹形小滑块的质量m=1kg，小滑块与斜面间的动摩擦因数μ=0.25。现小滑块以某一初速度从斜面底端上滑，同时在斜面底端正上方的小球以初速度3m/s水平抛出，经过一段时间，小球恰好垂直斜面方向落入凹槽，此时，小滑块还在上滑过程中。求小滑块运动的时间和小滑块的动能变化量。（已知sin37°＝0.6, cos37°＝0.8， g取10m/s²）