高中物理平抛运动计算题

地面上有一个半径为R的圆形跑道，高为h的平台边缘上的P点在地面上P′点的正上方，P′与跑道圆心O的距离为L（L>R），如图所示。跑道上停有一辆小车，现从P点水平抛出小沙袋，使其落入小车中（沙袋所受空气阻力不计）。问：

（1）若小车在跑道上运动，则沙袋被抛出时的初速度在什么范围内？
（2）若小车沿跑道顺时针做匀速圆周运动，当小车恰好经过A点时，将沙袋抛出，为使沙袋能在B处落入小车中，小车的速率v应满足什么条件？

如图所示是一辆汽车从高台水平飞出后所摄得的频闪照片,照片上的虚线为用铅笔画出的正方形格子,若汽车的长度是3.6 m,取,求:

(1)频闪的时间间隔t;
(2)汽车离开高台时的速度.

如图所示，位于竖直平面上的光滑圆弧轨道，半径为R，OB沿竖直方向，上端A距地面高度为H，质量为m的小球从A点由静止释放，到达B点时的速度为，最后落在地面上C点处，不计空气阻力，求：

（1）小球刚运动到B点时的加速度为多大，对轨道的压力多大 （2）小球落地点C与B点水平距离为多少。

如图所示，位于竖直平面上的1/4光滑轨道，半径为R，OB沿竖直方向，圆弧轨道上端A点距地面高度为H，质量为m的小球从A点由静止释放，最后落在地面C点处，不计空气阻力。求：

（1） 小球刚运动到B点时，轨道对小球的支持力多大?
（2） 小球落地点C与B的水平距离S为多少?
（3） 比值R/H为多少时，小球落地点C与B水平距离S最远? 该水平距离的最大值是多少?

钓鱼岛是我国固有领土，决不允许别国侵占，近期，为提高警惕保卫祖国，我国海军为此进行了登陆演练．如图所示，假设一艘战舰因吨位大吃水太深，只能停锚在离海岸登陆点s＝1km处．登陆队员需要从较高的军舰甲板上，利用绳索下滑到登陆快艇上再行登陆接近目标，若绳索两端固定好后，与竖直方向的夹角θ＝30°，为保证行动最快，队员甲先无摩擦自由加速滑到某最大速度，再靠摩擦匀减速滑至快艇，速度刚好为零，在队员甲开始下滑时，队员乙在甲板上同时开始向快艇以速度v₀＝m/s平抛救生圈，第一个刚落到快艇，接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇，若人的质量为m，重力加速度g＝10 m/s²，问：

（1）军舰甲板到快艇的竖直高度H及队员甲在绳索上运动的时间t₀；
（2）若加速过程与减速过程中的加速度大小相等，则队员甲在何处速度最大？最大速度是多大？
（3）若快艇额定功率为5 kW，载人后连同装备总质量为10³ kg，从静止开始以最大功率向登陆点加速靠近，到达岸边时刚好能达到最大速度10 m/s，快艇在水中受到的阻力恒定，求快艇运动的时间t′.

如图所示，一质量为M的物块静止在桌面边缘，桌面离水平地面的高度为h。一质量为m的子弹以水平速度v₀射入物块后，以水平速度射出.已知重力加速度为g，求：

（1）此过程中系统损失的机械能。
（2）此后物块落地点离桌面边缘的水平距离。

一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ＝37°，设乘客下滑过程绳索始终保持直线。为保证行动又快又安全，乘客先从静止开始匀加速滑到某最大速度，再匀减速滑至快艇，速度刚好为零，加速过程与减速过程中的加速度大小相等。在乘客开始下滑时，船员同时以水平速度向快艇抛出救生圈刚好落到救援快艇上（快艇可视为质点），如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍，不计空气阻力，重力加速度g取10 m/s²，sin37°= 0.6，cos37°=0.8，求：

（1）乘客沿着绳索下滑的时间t；
（2）乘客下滑过程的最大速度v_m。

为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其AB与BC轨道以微小圆弧相接，如图所示．一个小物块以初速度v₀＝4.0m/s从某一高处水平抛出，到A点时速度方向恰好沿AB方向，并沿倾斜轨道滑下．已知物块与倾斜轨道的动摩擦因数 μ = 0.50．（g＝10m/s²、sin37°＝ 0.60、cos37° ＝0.80）

⑴求小物块到达A点时速度。
⑵要使小物块不离开轨道，并从轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件？
⑶为了让小物块不离开轨道，并且能够滑回倾斜轨道AB，则竖直圆轨道的半径应该满足什么条件？

浙江卫视六频道《我老爸最棒》栏目中有一项人体飞镖项目，该运动简化模型如图所示。某次运动中，手握飞镖的小孩用不可伸长的细绳系于天花板下，在A处被其父亲沿垂直细绳方向推出，摆至最低处B时小孩松手，飞镖依靠惯性飞出击中竖直放置的圆形靶最低点D点，圆形靶的最高点C与B在同一高度，C、O、D在一条直径上，A、B、C三处在同一竖直平面内，且BC与圆形靶平面垂直。已知飞镖质量m=1kg，BC距离s=8m，靶的半径R=2m，AB高度差h=0.8m，g取10m/s²。不计空气阻力，小孩和飞镖均可视为质点。

（1）求孩子在A处被推出时初速度v_o的大小；
（2）若小孩摆至最低处B点时沿BC方向用力推出飞镖，飞镖刚好能击中靶心，求在B处小孩对飞镖做的功W;
（3）在第（2）小题中，如果飞镖脱手时沿BC方向速度不变，但由于小孩手臂的水平抖动使其获得了一个垂直于BC的水平速度v，要让飞镖能够击中圆形靶，求v的取值范围。

如图所示，装甲车在水平地面上以速度沿直线前进，车上机枪的枪管水平，距地面高为。在车正前方竖直一块高为两米的长方形靶，其底边与地面接触。枪口与靶距离为时，机枪手正对靶射出第一发子弹，子弹相对于枪口的初速度为。在子弹射出的同时，装甲车开始匀减速运动，行进后停下。装甲车停下后，机枪手以相同方式射出第二发子弹。（不计空气阻力，子弹看成质点，重力加速度）

（1）求装甲车匀减速运动时的加速度大小；

（2）当时，求第一发子弹的弹孔离地的高度，并计算靶上两个弹孔之间的距离；

（3）若靶上只有一个弹孔，求的范围。

图为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，表面粗糙的段与四分之一光滑圆弧轨道在点水平相切。点距水面的高度为H，圆弧轨道BC的半径为R，圆心恰在水面。一质量为的游客（视为质点）可从轨道的任意位置滑下，不计空气阻力。

（1）若游客从点由静止开始滑下，到点时沿切线方向滑离轨道落在水面点，，求游客滑到的速度大小及运动过程轨道摩擦力对其所做的功；

（2）若游客从段某处滑下，恰好停在点，有因为受到微小扰动，继续沿圆弧轨道滑到点后滑离轨道，求点离水面的高度。（提示：在圆周运动过程中任一点，质点所受的向心力与其速率的关系为)

如图所示，质量为m=1kg的小球用线长l＝1m的细线拴住，细绳上端固定在O点，当小球从图示M点释放后摆到悬点O的正下方N点时，细线恰好被拉断，此后小球刚好能无碰撞地从置于地面上倾角为45º的斜面滑下，已知斜面高度 h=0.4m，斜面左端离O点正下方的P点水平距离S=0.4m，不计空气阻力，求：

（1）N点距离地面的高度H  
（2）细绳能承受的最大拉力

一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ＝37°，设乘客下滑过程绳索始终保持直线。为保证行动又快又安全，乘客先从静止开始匀加速滑到某最大速度，再匀减速滑至快艇，速度刚好为零，加速过程与减速过程中的加速度大小相等。在乘客开始下滑时，船员同时以水平速度向快艇抛出救生圈刚好落到救援快艇上（快艇可视为质点），如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍，不计空气阻力，重力加速度g取10 m/s²，sin37°= 0.6，cos37°= 0.8，求：

（1）乘客沿着绳索下滑的时间t；
（2）乘客下滑过程的最大速度v_m。

一人用一根长L=1m，最大只能承受T=46N拉力的轻绳子，拴着一个质量m=1kg的小球（不考虑其大小），在竖直平面内作圆周运动，已知圆心O离地高H=21m，如图所示，若小球运动到达最低点时绳刚好被球拉断，求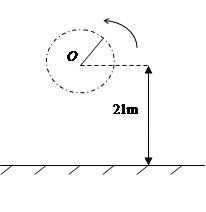

（1）小球到达最低点的速度大小是多少?   
（2）小球落地点到O点的水平距离是多少?（g=10m/s²）

）如图所示，某人骑摩托车在水平道路上行驶，要在A处越过x=5m的壕沟，沟面对面比A处低h=1.25m，（取g=10m/s²）求：

（1）摩托车在空中飞行的时间？
（2）摩托车的开始飞越壕沟的初速度至少要有多大？