如图所示,地面上有一高h的平台,平台下有一倾角可调的挡板,挡板的一端与平台边缘A点的正下方B点重合。将一个可视为质点的小球以v的速度水平推出。适当调节挡板的倾角,小球会刚好垂直撞在挡板上。已知小球下落过程中所受空气阻力忽略不计,当地重力加速度为g。求小球运动的时间是多少?
如图所示,质量为2kg的金属块放在水平地面上,在大小为20N、方向与水平方向成37°角的斜向上拉力F作用下,从静止开始做匀加速直线运动.已知金属块与地面间的动摩擦因数μ=0.5,力F持续作用2s后撤去。(sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2).求:金属块在地面上总共滑行了多远?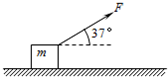
(1)实验小组用如图所示的装置“探究功与物体速度变化的关系”,某同学分别取1条、2条、3条…同样的橡皮筋进行第1次、第2次、第3次…实验,每次每根橡皮筋拉伸的长度都保持一致,则每次橡皮筋对小车做的功记作W0、2W0、3W0…,下列说法正确的是_____________
| A.为减小实验误差,长木板应水平放置 |
| B.通过增加橡皮筋的条数可以使橡皮筋对小车做的功成整数倍增加 |
| C.小车在橡皮筋拉力作用下做匀加速直线运动,当橡皮筋恢复原长后小车做匀速运动 |
| D.应选择纸带上点距均匀的一段计算小车的速度 |
(2)某同学把每次橡皮筋对小车做的功记作W0、2W0、3W0……,对每次打出的纸带进行处理,获得v,v2的数值记录在表格中。
| W |
0 |
W0 |
2W0 |
3W0 |
4W0 |
5W0 |
6W0 |
| v/(m·s-1) |
0 |
1.0 |
1.4 |
1.7 |
2.0 |
2.2 |
2.4 |
| v2/(m2·s-2) |
0 |
1 |
1.9 |
|
|
|
|
请你根据表中的数据作出W-v、W-v2图线。
由图线探究功与物体速度变化的关系是 。
某物理兴趣小组在探究平抛运动的规律实验时,将小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到了如图所示的照片,但照片上有一破损处.已知每个小方格边长9.8cm,当地的重力加速度为g=9.8m/s2.(结果保留三位有效数字)
(1)若以拍摄的第1个点为坐标原点,水平向右和竖直向下为正方向,则照片上破损处的小球位置坐标为 X= cm ,Y= cm.
(2)小球平抛的初速度大小为 .
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6),以最低点C所在的水平面为重力势能的参考平面,则
A.A、B两球所受弹力的大小之比为4︰3
B.A、B两球运动的周期之比为4︰3
C.A、B两球的动能之比为64︰27
D.A、B两球的重力势能之比为16︰9
质量为m的汽车以恒定功率P启动后沿水平道路行驶,经过一段时间后将达到最大速度v。若行驶中受到的摩擦阻力大小不变,则在加速过程中车速为v/3时,汽车的加速度大小为
| A.3P/mv | B.2P/mv | C.P/mv | D.4P/mv |
设地球自转周期为T,质量为M。引力常量为G。假设地球可视为质量均匀分布的球体,半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为
A. |
B. |
C. |
D. |
图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x="1" m处的质点,Q是平衡位置为x="4" m处的质点,图乙为质点Q的振动图象,则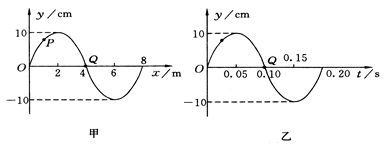
| A.波向-x方向传播 |
| B.该波的波速为40m/s |
| C.t=0.10时刻质点P正向平衡位置运动 |
| D.t=0.075s时刻质点P运动至平衡位置 |
如图所示为一水平方向弹簧振子的振动图象,弹簧的劲度系数为20 N/cm,下列说法正确的是 
| A.在0~4 s内振子做了1.75次全振动 |
| B.在0~4 s内振子通过的路程为35 cm |
| C.图中A点对应的时刻振子的速度方向指向+x轴方向,且处于减速运动阶段 |
| D.图中A点对应的时刻振子所受的弹力大小为50 N,方向指向+x方向 |
如图所示,在直角坐标系中 的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求
的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求
(1)磁感应强度的大小;
(2)粒子从x轴上出射的区域范围;
(3)能离开磁场的粒子个数与粒子源发射粒子总数的比值.
如图所示,一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度转动,盘面上离转轴距离r=0.1m处有一质量为0.1kg的小物体恰好能与圆盘始终保持相对静止.物体与盘面间的动摩擦因数为0.8(设最大静摩擦力等于滑动摩擦力),盘面与水平面的夹角为37°(g=10m/s2,sin37°=0.6),求:
(1)圆盘转动的角速度ω的大小;
(2)小物体运动到最高点时受到的摩擦力.
已知火星质量约为地球质量的0.1倍 ,火星表面附近引力加速度约为地表附近重力加速度的0.4倍.将火星和地球的半径比记为k,火星的近地卫星和地球的近地卫星的环绕速度之比记为n,则
A. |
B. |
C. |
D. |
如图所示,光滑水平面上静止着半径相同的三个小球A.B.C,其中小球A.C的质量分别为mA=m,mC=4m。现使A以初速v0沿B.C连线方向向B运动,问B球的质量M为何值时,才能使C球碰撞后的速度最大?(已知A.B.C之间的碰撞均为弹性碰撞)
如图所示,质量M="4" kg的滑板B静止放在光滑水平面上,其右端固定一根水平轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,这段滑板与木块A(可视为质点)之间的动摩擦因数μ=0.2,而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。小木块A以速度v0=10m/s,由滑板B左端开始沿滑板水平上表面向右运动。已知木块A的质量m="1" kg,g取 10m/s2。求
(1)弹簧被压缩到最短时木块A的速度;
(2)木块A压缩弹簧过程中弹簧弹性势能的最大值为多少?