如图所示,在直角坐标系中 的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求
的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求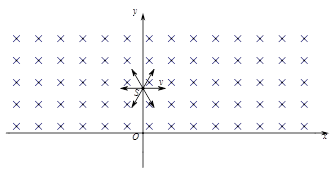
(1)磁感应强度的大小;
(2)粒子从x轴上出射的区域范围;
(3)能离开磁场的粒子个数与粒子源发射粒子总数的比值.
如图所示,在直角坐标系中 的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求
的范围内有垂直于坐标平面向内且范围足够长的匀强磁场.在y 轴上S 点(0,d) 处有一粒子源,向坐标平面内各个方向等概率的发射速率均为v的带电粒子,粒子电量均为-q,质量均为m.已知速度沿+y方向的带电粒子恰好不会离开磁场.不计粒子重力,求
(1)磁感应强度的大小;
(2)粒子从x轴上出射的区域范围;
(3)能离开磁场的粒子个数与粒子源发射粒子总数的比值.