如图所示，质量M="4" kg的滑板B静止放在光滑水平面上，其右端固定一根水平轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5m，这段滑板与木块A(可视为质点）之间的动摩擦因数μ=0.2，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。小木块A以速度v0=10m/s，由滑板B左端开始沿滑板水平上表面向右运动。已知木块A的质量m="1" kg，g取 10m/s2。求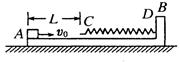
（1）弹簧被压缩到最短时木块A的速度；
（2）木块A压缩弹簧过程中弹簧弹性势能的最大值为多少？
如图所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角θ＝30°，导轨电阻不计。磁感应强度为B=2T的匀强磁场垂直导轨平面向上，长为L=0.5m的金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨电接触良好，金属棒ab的质量m=1kg、电阻r=1Ω。两金属导轨的上端连接右端电路，灯泡电阻RL＝4Ω，定值电阻R1＝2Ω，电阻箱电阻R2＝12Ω，重力加速度为g="10" m/s2，现闭合开关，将金属棒由静止释放，下滑距离为s0=50m时速度恰达到最大，试求：
（1）金属棒下滑的最大速度vm；
（2）金属棒由静止开始下滑2s0的过程中整个电路产生的电热Q。
如图所示，无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上，轨道间距L="1" m，底部接入一阻值为R=0.4Ω的定值电阻，上端开口。垂直斜面向上的匀强磁场的磁感应强度B=2T。一质量为m=0.5kg的金属棒ab与导轨接触良好，ab与导轨间动摩擦因数μ=0.2，ab连入导轨间的电阻r=0.1Ω，电路中其余电阻不计。现用一质量为M=2.86kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连。由静止释放M，当M下落高度h="2.0" m时，ab开始匀速运动（运动中ab始终垂直导轨，并接触良好）。不计空气阻力，sin53°=0.8，cos53°=0.6，取g=10m/s2。求：
（1）ab棒沿斜面向上运动的最大速度vm；
（2）ab棒从开始运动到匀速运动的这段时间内电阻R上产生的焦耳热QR和流过电阻R的总电荷量q。
如图所示，在足够长的绝缘板MN上方距离为d的O点处，水平向左发射一个速率为v0，质量为
、电荷为
的带正电的粒子（不考虑粒子重力）。
（1）若在绝缘板上方加一电场强度大小为
、方向竖直向下的匀强电场，求带电粒子打到板上距P点的水平距离（已知
）；
（2）若在绝缘板的上方只加一方向垂直纸面，磁感应强度
的匀强磁场，求：①带电粒子在磁场中运动半径； ②若O点为粒子发射源，能够在纸面内向各个方向发射带电粒子（不考虑粒子间的相互作用），求发射出的粒子打到板上的最短时间。
如图甲所示，电阻不计，间距为
的平行长金属导轨置于水平面内，阻值为
的导体棒
固定连接在导轨左端，另一阻值也为的导体棒
垂直放置到导轨上，与导轨接触良好，并可在导轨上无摩擦移动。现有一根轻杆一端固定在中点，另一端固定于墙上，轻杆与导轨保持平行，
两棒间距为
。若整个装置处于方向竖直向下的匀强磁场中，且从某一时刻开始，磁感应强度
随时间
按图乙所示的方式变化。
（1）求在0～
时间内流过导体棒的电流的大小与方向；
（2）求在
时间内导体棒产生的热量；
（3）1.5时刻杆对导体棒的作用力的大小和方向。
如图所示，足够大的荧光屏ON垂直xOy坐标面，与x轴夹角为30°，当y轴与ON间有沿+y方向、场强为E的匀强电场时，一质量为m、电荷量为-q的离子从y轴上的P点，以速度v0、沿+x轴方向射入电场，恰好垂直打到荧光屏上的M点（图中未标出）．现撤去电场，在y轴与ON间加上垂直坐标面向里的匀强磁场，相同的离子仍以速度v0从y轴上的Q点沿+x轴方向射入磁场，恰好也垂直打到荧光屏上的M点，离子的重力不计．求：
（1）离子在电场中运动的时间t1；
（2）P点距O点的距离y1和离子在磁场中运动的加速度大小a；
（3）若相同的离子分别从y轴上的不同位置以速度
（
，k为常数）、沿+x轴方向射入磁场，离子都能打到荧光屏上，k应满足的条件．
粤公网安备 44130202000953号