已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n个数是n).设这组数据的各数之和是s,中位数是k,则s= (用只含有k的代数式表示).
如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有 根小棒.
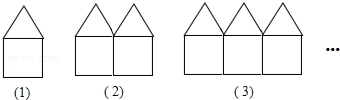
对于正数x,规定f(x)= ,例如f(3)=
,例如f(3)=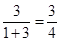 ,f(
,f( )=
)=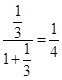 ,计算f(
,计算f( )+ f(
)+ f( )+ f(
)+ f(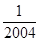 )+ …f(
)+ …f( )+ f(
)+ f(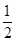 )+f(1)+f(1)+f(2)+f(3)+…+ f(2004)+f(2005)+f(2006)= .
)+f(1)+f(1)+f(2)+f(3)+…+ f(2004)+f(2005)+f(2006)= .
请阅读下列材料:若两个正实数a1,a2满足a12+a22=1,那么a1+a2≤ .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤ .
.
根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为________.