请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤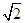
.
证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.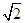
根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．
相关试题
在R上存在导数
,对任意的
有
,且在
上
.若
,则实数
的取值范围 .
上,若圆M上不存在点N，使
,其中A（0，3），则圆心M横坐标的取值范围 .
的最大值是 .
，则∠BDF的正切值 推荐套卷
请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤.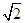
证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.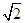
根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．
粤公网安备 44130202000953号