高三数学第五套
已知x,y的取值如右表:从散点图可以看出y与x线性相关,且回归方程为 ,则
,则 ( )
( )
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
A.3.25 B.2.6 C.2.2 D.0
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )

A. |
B. |
C. |
D. |
在某项测量中,测量结果 服从正态分布
服从正态分布 ,若
,若 在(0,2)内取值的概率为0.4,则
在(0,2)内取值的概率为0.4,则 在(0,+∞)内取值的概率为( )
在(0,+∞)内取值的概率为( )
| A.0.2 | B.0.4 | C.0.8 | D.0.9 |
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为 ( )

| A.24种 | B.48种 | C.72种 | D.96种 |
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件 与
与 同时发生的概率是( )
同时发生的概率是( )
A. |
B. |
C. |
D. |
某单位为了了解用电量 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量 (度) (度) |
25 |
35 |
37 |
63 |
(本小题满分10分)某校高一年级开设 ,
, ,
, ,
, ,
, 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程;
的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值: )
)
 的共轭复数的虚部为 ( )
的共轭复数的虚部为 ( )



 时,在验证n=1成立时,左边应该是( )
时,在验证n=1成立时,左边应该是( ) 的二项展开式中,x的系数为( )
的二项展开式中,x的系数为( ) 的分布列如表:则
的分布列如表:则 ( )
( )










 B.
B. C.
C. D.
D.
 为奇函数,且
为奇函数,且 是
是 的一个零点,则
的一个零点,则 一定是下列哪个函数的零点 ( )
一定是下列哪个函数的零点 ( ) 



 的展开式中
的展开式中 的系数是-35,则
的系数是-35,则 = .
= . 在点
在点 处的切线方程为________.
处的切线方程为________. 的展开式的第二项的系数为
的展开式的第二项的系数为 ,则
,则 的值为 .
的值为 . ,可以采用以下方法:
,可以采用以下方法: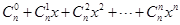
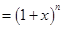 ,两边对x求导,
,两边对x求导,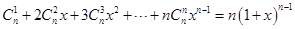 ,
, ,得
,得 .类比上述计算方法,计算
.类比上述计算方法,计算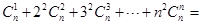 .
. ;
; 求
求 的值;
的值; 求实数
求实数 的值.
的值.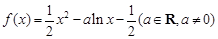 .
. 时,求曲线
时,求曲线 在点
在点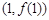 处的切线方程;
处的切线方程; 的单调区间;
的单调区间;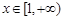 ,都有
,都有 成立,求a的取值范围.
成立,求a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号