高中数学填空题

4. 设函数的定义域为，如果对于任意的，存在唯一的，使（为常数）成立，则称函数在上的均值为，请写出满足在其定义域上均值为1的两个函数___________  

在直四棱柱A₁B₁C₁D₁—ABCD中，当底面四边形ABCD满足条件        时，有A₁C⊥B₁D₁（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形）．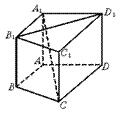

若干个能惟一确定一个数列的量称为该数列的“基本量”．设是公比为q的无穷等比数列，下列的四组量中，一定能成为该数列“基本量”的是第        组．（写出所有符合要求的组号）．①S₁与S₂；②a₂与S₃；③a₁与a_n；④q与a_n．(其中n为大于1的整数，S_n为的前n项和．)

设函数是偶函数，则t的一个可能值是     ．

设a是整数，0≤b＜1．若a²＝2b(a＋b)，则b＝           ．

设数列{a_n}满足：a_n＋1a_n＝2a_n＋1－2(n＝1，2，…)，a₂₀₀₉＝，则此数列的前2009项的和为        ．

右图是某种净水水箱结构的设计草图，其中净水器是一个宽10cm、体积为3000cm³的长方体，长和高未定．净水水箱的长、宽、高比净水器的长、宽、高分别长20cm、20cm、60cm．若不计净水器中的存水，则净水水箱中最少可以存水             cm³．

设f(x)＝log₃x－，则满足f(x)≥0的x的取值范围是           ．

如图，在四面体ABCD中，P、Q分别为棱BC与CD上的点，且BP＝2PC，CQ＝2QD．R为棱AD的中点，则点A、B到平面PQR的距离的比值为         ．

已知等差数列{a_n}的前11项的和为55，去掉一项a_k后，余下10项的算术平均值为4．若a₁＝－5，则k＝         ．

已知sinαcosβ＝1，则cos(α＋β)＝          ．

一个半径为1的小球在一个内壁棱长为的正四面体容器内可向各个方向自由运动，则该小球永远不可能接触到的容器内壁的面积是．

设数列的前项和满足：，，则通项=_____．

将24个志愿者名额分配给3个学校，则每校至少有一个名额且各校名额互不相同的分配方法共有　　　种．

设的最小值为，则