分类变量X和Y的列联表如下:
| |
Y1 |
Y2 |
总计 |
| X1 |
a |
b |
a+b |
| X2 |
c |
d |
c+d |
| 总计 |
a+c |
b+d |
a+b+c+d |
则下列说法正确的是________.
①ad-bc越小,说明X与Y关系越弱;
②ad-bc越大,说明X与Y关系越强;
③(ad-bc)2越大,说明X与Y关系越强;
④(ad-bc)2越接近于0,说明X与Y关系越强.
计算下面事件A与事件B的2×2列联表的χ2统计量值,得χ2≈________,从而得出结论________.
| |
B |
 |
总计 |
| A |
39 |
157 |
196 |
 |
29 |
167 |
196 |
| 总计 |
68 |
324 |
392 |
若线性回归方程中的回归系数 =0,则相关系数r=________.
=0,则相关系数r=________.
已知对一组观测值(xi,yi)(i=1,2,…,n)作出散点图后,确定具有线性相关关系,若对于 =
= +
+ x,求得
x,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________.
由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到线性回归方程 =
= x+
x+ ,那么下列说法正确的是________.
,那么下列说法正确的是________.
①直线 =
= x+
x+ 必经过点(
必经过点( ,
, );
);
②直线 =
= x+
x+ 至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③直线 =
= x+
x+ 的斜率为
的斜率为 ;
;
④直线 =
= x+
x+ 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差 是该坐标平面上的直线与这些点的最小偏差.
是该坐标平面上的直线与这些点的最小偏差.
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 |
1 |
2 |
3 |
4 |
5 |
| x |
169 |
178 |
166 |
175 |
180 |
| y |
75 |
80 |
77 |
70 |
81 |
(1)已知甲厂生产的产品共98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足≥175且y≥75,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随即抽取2件,求抽取的2件产品中优等品数X的分布列及其均值(即数学期望).
一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个,则其中含红球个数的数学期望是________.
在一次考试中,某班语文、数学、外语平均分在80分以上的概率分别为 、
、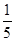 、
、 ,则该班的三科平均分都在80分以上的概率是________.
,则该班的三科平均分都在80分以上的概率是________.
设数列 的前n项和为
的前n项和为 ,令
,令 ,称
,称 为数列
为数列 的“理想数”.(1)数列
的“理想数”.(1)数列 的“理想数”是 ;(2)若数列
的“理想数”是 ;(2)若数列 的“理想数”是2013,则数列
的“理想数”是2013,则数列 的“理想数”是 .
的“理想数”是 .
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为
 ,圆C的参数方程为
,圆C的参数方程为
 ,P点在圆C上,则点P到直线
,P点在圆C上,则点P到直线 的距离的最大值与最小值的和为 .
的距离的最大值与最小值的和为 .
已知数列 满足
满足 ,
, ,定义:使乘积
,定义:使乘积 为正整数的k
为正整数的k 叫做“简易数”.则在[3,2013]内所有“简易数”的和为 .
叫做“简易数”.则在[3,2013]内所有“简易数”的和为 .