某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元,(其他因素不考虑)计算收费标准的框图如图所示,则①处应填 ;

某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分, 先收取固定的制版费,再按印刷数量收取印刷费;乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量 x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个____ 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用 与证书数量x之间的函数关系式为 ;
与证书数量x之间的函数关系式为 ;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由
已知抛物线 经过点
经过点 和
和 .下列结论:
.下列结论:
 ;
;
 ;
;
③当 时,抛物线与x轴必有一个交点在点(1,0)的右侧;
时,抛物线与x轴必有一个交点在点(1,0)的右侧;
④抛物线的对称轴为
其中结论正确的有__________________(写出所有正确结论的番号)
某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6,则应从一年级本科生中抽取________名学生.
某班有50名同学参加跳远和铅球比赛,跳远和铅球及格的人数分别是40与31人,两项都不及格的人数为4人,则两项都及格的人数是________.
对于三次函数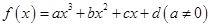 ,给出定义:
,给出定义: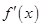 是函数
是函数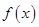 的导函数,
的导函数, 是
是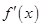 的导函数,若方程
的导函数,若方程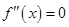 有实数解
有实数解 ,则称点
,则称点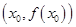 为函数
为函数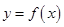 的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有都有对称中心,且“拐点”就是对称中心.若
的“拐点”.某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有都有对称中心,且“拐点”就是对称中心.若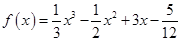 ,根据这一发现,可求得
,根据这一发现,可求得
甲、乙两个小组各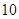 名学生的英语口语测试成绩的茎叶图如图所示.现从这
名学生的英语口语测试成绩的茎叶图如图所示.现从这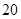 名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件
名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件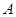 ;“抽出的学生英语口语测试成绩不低于
;“抽出的学生英语口语测试成绩不低于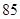 分”记为事件
分”记为事件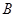 .则
.则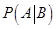 的值是________.
的值是________.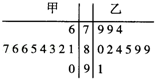
抛物线 的焦点为
的焦点为 ,过点
,过点 的直线与该抛物线相交于
的直线与该抛物线相交于 两点,直线
两点,直线 分别交抛物线于点
分别交抛物线于点 .若直线
.若直线 的斜率分别为
的斜率分别为 ,则
,则 _____.
_____.
某地区打的士收费办法如下:不超过2公里收7元,超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元,(其他因素不考虑)计算收费标准的框图如图所示,则①处应填 ;

某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示。现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第3组的人数是 ;
,得到的频率分布直方图如图所示。现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第3组的人数是 ;

某单位有青年职工、中年职工、老年职工共900人,其中青年职工450人,为迅速了解职工的家庭状况,采用分层抽样的方法从中抽取样本,若样本中的青年职工为15人,则抽取的样本容量为 .