设F1,F2分别是椭圆E:x2+ =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求|AB|;
(2)若直线l的斜率为1,求b的值.
已知椭圆中心在坐标原点,焦点在x轴上,离心率为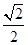 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点.
(1)求椭圆方程;
(2)若直线y=x-1与抛物线相切于点A,求以A为圆心且与抛物线的准线相切的圆的方程;
(3)若斜率为1的直线交椭圆于M、N两点,求△OMN面积的最大值(O为坐标原点).
已知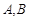 分别是椭圆
分别是椭圆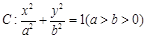 的左,右顶点,点
的左,右顶点,点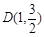 在椭圆
在椭圆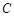 上,且直线
上,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(1)求椭圆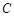 的标准方程;
的标准方程;
(2)点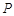 为椭圆
为椭圆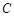 上除长轴端点外的任一点,直线
上除长轴端点外的任一点,直线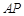 ,
,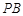 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点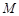 ,
,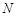 .
.
①在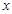 轴上是否存在一个定点
轴上是否存在一个定点 ,使得
,使得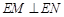 ?若存在,求点
?若存在,求点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②已知常数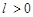 ,求
,求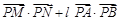 的取值范围.
的取值范围.
已知椭圆 :
: 的左焦点为
的左焦点为 ,且过点
,且过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点P(-2,0)的直线与椭圆E交于A、B两点,且满足 .
.
①若 ,求
,求 的值;
的值;
②若M、N分别为椭圆E的左、右顶点,证明: 
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若方程 有解,求实数m的取值范围;
有解,求实数m的取值范围;
(3)若存在实数 ,使
,使 成立,求证:
成立,求证: .
.
已知双曲线 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,点
的准线上,点 是双曲线
是双曲线 右支上相异两点,且满足
右支上相异两点,且满足
 为线段
为线段 的中点,直线
的中点,直线 的斜率为
的斜率为
(1)求双曲线 的方程;
的方程;
(2)用 表示点
表示点 的坐标;
的坐标;
(3)若 ,
, 的中垂线交
的中垂线交 轴于点
轴于点 ,直线
,直线 交
交 轴于点
轴于点 ,求
,求 的面积的取值范围.
的面积的取值范围.
已知函数 是奇函数,(其中
是奇函数,(其中 )
)
(1)求实数m的值;
(2)在 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性;
(3)当x 时,f(x)的值域是(1,
时,f(x)的值域是(1, ),求n与a的值。
),求n与a的值。
已知双曲线x2-y2=2若直线n的斜率为2 ,直线n与双曲线相交于A、B两点,线段AB的中点为P,
(1)求点P的坐标(x,y)满足的方程(不要求写出变量的取值范围);
(2)过双曲线的左焦点F1,作倾斜角为 的直线m交双曲线于M、N两点,期中
的直线m交双曲线于M、N两点,期中 ,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角
,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角 的表达式。
的表达式。
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设 .
.
(1)试用 表示
表示 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
已知点 、
、 为双曲线
为双曲线 :
: 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点 ,且
,且 .圆
.圆 的方程是
的方程是 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、 ,求
,求 的值;
的值;
(3)过圆 上任意一点
上任意一点 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于 、
、 两点,
两点, 中点为
中点为 ,求证:
,求证: .
.
已知函数f(x)= .
.
(1)函数f(x)在点(0,f(0))的切线与直线2x+y-1=0平行,求a的值;
(2)当x∈[0,2]时,f(x)≥ 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足 =
= ,O为坐标原点.
,O为坐标原点.
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
已知函数f(x)=ex-kx2,x∈R.
(1)若k=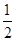 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1;
(2)若f(x)在区间(0,+∞)上单调递增,试求k的取值范围;
(3)求证: <e4(n∈N*)..
<e4(n∈N*)..
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
(1)证明:平面EAC⊥平面PBD;
(2)若PD∥平面EAC,并且二面角B-AE-C的大小为45°,求PD∶AD的值.
设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+ ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.