高中数学解答题

上海理）给定常数，定义函数，数列满足.
（1）若，求及；
（2）求证：对任意，；
（3）是否存在，使得成等差数列？若存在，求出所有这样的，若不存在，说明理由.

广东理）设函数(其中).
(1) 当时,求函数的单调区间；
(2) 当时,求函数在上的最大值.

已知椭圆G：．过点(m，0)作圆的切线l交椭圆G于A，B两点．
(1)求椭圆G的焦点坐标和离心率；
(2)将表示为m的函数，并求的最大值．

已知点，圆C：与椭圆E:有一个公共点，分别是椭圆的左、右焦点，直线与圆C相切．

（1）求m的值与椭圆E的方程；
（2）设Q为椭圆E上的一个动点，求的取值范围．

如图，动点与两定点、构成，且，设动点的轨迹为．

（1）求轨迹的方程；
（2）设直线与轴相交于点，与轨迹相交于点，且，求的取值范围．

已知双曲线的中心在原点，离心率为2，一个焦点为F(－2，0)．
(1)求双曲线方程；
(2)设Q是双曲线上一点，且过点F，Q的直线l与y轴交于点M，若= 2，求直线l的方程．

如图，已知双曲线的左、右顶点分别为A₁、A₂，动直线l：y＝kx＋m与圆相切，且与双曲线左、右两支的交点分别为．

(1)求k的取值范围，并求的最小值；
(2)记直线的斜率为，直线的斜率为，那么是定值吗？证明你的结论．

已知顶点为原点的抛物线的焦点与椭圆的右焦点重合,与在第一和第四象限的交点分别为.
(1)若是边长为的正三角形，求抛物线的方程；
(2)若，求椭圆的离心率.

已知函数.
(1)求函数在上的最大值和最小值；
(2)求证：当时，函数的图像在的下方．

已知首项为的等比数列不是递减数列，其前n项和为，且成等差数列。
（1）求数列的通项公式；
（2）设，求数列的最大项的值与最小项的值。

在中，角为锐角，已知内角、、所对的边分别为、、，向量且向量共线．
（1）求角的大小；
（2）如果，且,求.

一个三角形数表按如下方式构成（如图：其中项数）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如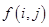：；为数表中第行的第个数．
（1）求第2行和第3行的通项公式和；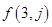
（2）证明：数表中除最后2行外每一行的数都依次成等差数列；
（3）求关于（）的表达式．

已知函数（），且函数图象过原点.
（Ⅰ）求函数的单调区间；
（Ⅱ）函数在定义域内是否存在零点？若存在，请指出有几个零点；若不存在，请说明理由.

已知函数（），且函数图象过原点.
（Ⅰ）求函数的单调区间；
（Ⅱ）函数在定义域内是否存在零点？若存在，请指出有几个零点；若不存在，请说明理由；
（Ⅲ）若，当时，不等式恒成立，求a的取值范围．

如图，已知椭圆Γ：＋＝1（a＞b＞0）的左、右焦点分别是F₁（－c，0）、F₂（c，0），Q是椭圆外的一个动点，满足||＝2a．点P是线段F₁Q与该椭圆的交点，点M在线段F₂Q上，且满足·＝0，||≠0．

（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设不过原点O的直线l与轨迹C交于A，B两点，若直线OA，AB，OB的斜率依次成等比数列，求△OAB面积的取值范围；
（Ⅲ）由（Ⅱ）求解的结果，试对椭圆Γ写出类似的命题．（只需写出类似的命题，不必说明理由）