已知抛物线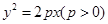 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的一个交点,且
有相同的焦点F,点A是两曲线的一个交点,且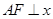 轴,若
轴,若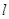 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则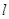 的倾斜角所在的区间可能是( )
的倾斜角所在的区间可能是( )
A.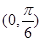 |
B.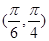 |
C.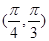 |
D.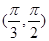 |
已知函数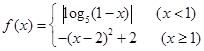 ,则关于
,则关于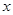 的方程
的方程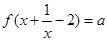 的实根个数不可能为( )
的实根个数不可能为( )
A.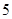 个 个 |
B.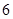 个 个 |
C.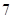 个 个 |
D.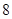 个 个 |
已知双曲线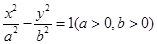 的右焦点为
的右焦点为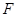 ,过
,过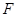 作斜率为
作斜率为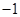 的直线交双曲线的渐近线于点
的直线交双曲线的渐近线于点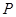 ,点
,点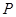 在第一象限,
在第一象限,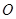 为坐标原点,若
为坐标原点,若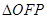 的面积为
的面积为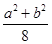 ,则该双曲线的离心率为
,则该双曲线的离心率为
A.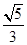 |
B.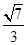 |
C.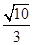 |
D.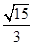 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x |
3 |
4 |
5 |
6 |
| 加工的时间y |
2.5 |
3 |
4 |
4.5 |
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是( )
A.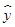 =0.7x+0.35 B.
=0.7x+0.35 B.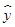 =0.7x+1
=0.7x+1
C.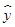 =0.7x+2.05 D.
=0.7x+2.05 D.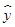 =0.7x+0.45
=0.7x+0.45
已知函数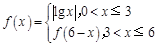 ,设方程
,设方程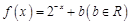 的四个实根从小到大依次为
的四个实根从小到大依次为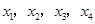 ,对于满足条件的任意一组实根,下列判断中一定正确的为( )
,对于满足条件的任意一组实根,下列判断中一定正确的为( )
A.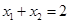 |
B.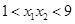 |
C. |
D.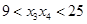 |
甲、乙两人下棋,两人下成和棋的概率是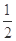 ,乙获胜的概率是
,乙获胜的概率是 ,则
,则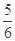 是( )
是( )
| A.乙胜的概率 | B.乙不输的概率 |
| C.甲胜的概率 | D.甲不输的概率 |
已知函数f(x)的定义域为[-1,5],部分对应值如下表.
| x |
-1 |
0 |
4 |
5 |
| f(x) |
1 |
2 |
2 |
1 |
f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题: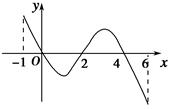
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中真命题的个数是 ( )
A.4 B.3 C.2 D.1
已知函数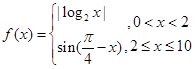 ,若存在实数
,若存在实数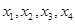 ,且
,且 则
则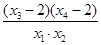 的取值范围是( )
的取值范围是( )
| A.(0,12) | B.(4.16) | C.(9,21) | D.(15,25) |
【原创】已知函数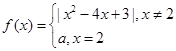 ,若方程
,若方程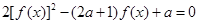 有9个不同的实数解,则实数
有9个不同的实数解,则实数 的取值范围是( )
的取值范围是( )
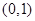 B.
B.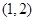 C.
C.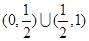 D.
D.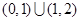
已知双曲线 :
: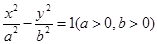 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于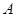 ,
,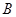 两点,
两点,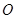 为坐标原点,若双曲线
为坐标原点,若双曲线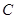 的离心率为2,
的离心率为2,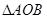 的面积为
的面积为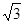 ,则
,则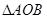 的内切圆半径为( )
的内切圆半径为( )
A.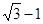 |
B.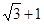 |
C.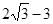 |
D.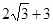 |
【改编】函数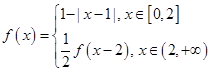 ,则下列命题中正确命题的个数是 ( ).
,则下列命题中正确命题的个数是 ( ).
①函数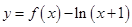 有
有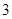 个零点;
个零点;
②若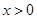 时,函数
时,函数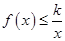 恒成立,则实数
恒成立,则实数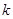 的取值范围是
的取值范围是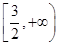 ;
;
③函数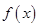 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④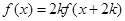
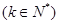 ,对一切
,对一切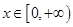 恒成立.
恒成立.
A.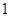 |
B.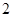 |
C.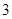 |
D.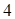 |
已知椭圆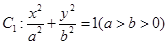 与圆
与圆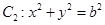 ,若在椭圆
,若在椭圆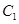 上存在点P,过P作圆的切线PA,PB,切点为A,.B使得
上存在点P,过P作圆的切线PA,PB,切点为A,.B使得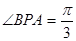 ,则椭圆
,则椭圆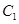 的离心率的取值范围是( )
的离心率的取值范围是( )
A.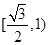 |
B.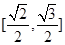 |
C.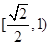 |
D.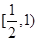 |