已知奇函数
在R上是增函数.若
),
,
,则a,b,c的大小关系为( )
A. B. C. D.
已知双曲线
的右焦点为F,点A在双曲线的渐近线上,
是边长为2的等边三角形(O为原点),则双曲线的方程为( )
A. B. C. D.
阅读如图的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为( )
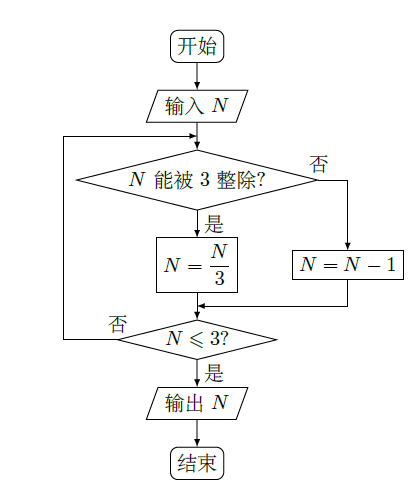
| A. | 0 |
B. | 1 |
C. | 2 |
D. | 3 |
有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为( )
A.
B.
C.
D.
设
,则"
"是"
"的( )
A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件
设 A, B是椭圆 C: 1长轴的两个端点,若 C上存在点 M满足∠ AMB=120°,则 m的取值范围是( )
| A. |
(0,1]∪[9,+∞) |
B. |
(0, ]∪[9,+∞) |
| C. |
(0,1]∪[4,+∞) |
D. |
(0, ]∪[4,+∞) |
△ ABC的内角 A, B, C的对边分别为 a, b, c,已知sin B+sin A(sin C﹣cos C)=0, a=2, c ,则 C=( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图程序框图是为了求出满足3 n﹣2 n>1000的最小偶数 n,那么在  和
和  两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
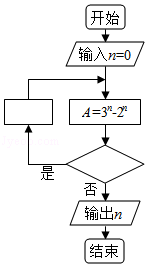
| A. |
A>1000和n=n+1 |
B. |
A>1000和n=n+2 |
| C. |
A≤1000和n=n+1 |
D. |
A≤1000和n=n+2 |
已知函数 f( x)= lnx+ ln(2﹣ x),则( )
| A. |
f(x)在(0,2)单调递增 |
| B. |
f(x)在(0,2)单调递减 |
| C. |
y=f(x)的图象关于直线x=1对称 |
| D. |
y=f(x)的图象关于点(1,0)对称 |
设 x, y满足约束条件 ,则 z= x+ y的最大值为( )
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
如图,在下列四个正方体中, A, B为正方体的两个顶点, M, N, Q为所在棱的中点,则在这四个正方体中,直线 AB与平面 MNQ不平行的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
已知 F是双曲线 C: x 2 1的右焦点, P是 C上一点,且 PF与 x轴垂直,点 A的坐标是(1,3),则△ APF的面积为( )
| A. |
|
B. |
|
C. |
|
D. |
|